Binary Search Trees
From
(→Inserting an Element into a Binary Search Tree) |
(→Example Binary Search Tree) |
||
| Line 7: | Line 7: | ||
</blockquote> | </blockquote> | ||
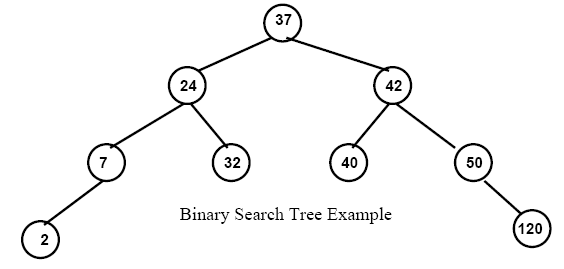
== Example Binary Search Tree == | == Example Binary Search Tree == | ||
| - | . | + | |
| - | <br | + | [[Image:BSTreeExample.png]] |
| + | |||
| + | |||
| + | |||
| + | <br><br> | ||
== Searching for an Element in a Binary Search Tree == | == Searching for an Element in a Binary Search Tree == | ||
Revision as of 16:08, 28 March 2009
An important and frequently used specialization of a binary tree is a Binary Search Tree. A binary search tree contains data that is comparable, for example numbers or text, and has the following property:
Binary Search Tree Property: If N is a node in the tree, and N contains data D, then all nodes in the left subtree of N contain data that is less than or equal to D and all nodes in the right subtree of N contain data that is greater than D.
Contents |
Example Binary Search Tree
Searching for an Element in a Binary Search Tree
Suppose I want to know if a value X is in the tree. I can search for X using the following algorithm.
LET Found = false
LET P = the root of the tree
WHILE not Found and P is not NULL do
IF P.Data equals X
set Found to TRUE
ELSE IF P.Data < X
set P to P.right
ELSE
set P to P.left
ENDIF
ENDWHILE
Why is a search tree such a good organization for data? Suppose I have a list of names that are stored in a binary search tree and suppose there are 1,000,000 names in the tree. I am given a name, and I want to know if that name is in the list. What is the most number of checks I will have to make to determine if the name is in the list or not? At most, log2(1,000,000) = 20 checks will have to be made.
Inserting an Element into a Binary Search Tree
Let P be a pointer to a tree node that is to be inserted into the tree. And, let Q be another pointer to a tree node that is initialized to the root of the tree.
IF Q is NULL, THEN
The node that is pointed to by P becomes the root of the tree.
ELSE
Let Inserted be a Boolean value initialized to False
ENDIF
WHILE (not Inserted)
IF (P.Data <= Q.Data)
If (Q.Left is null)
Set Q.Left to P
Set Inserted to True
ELSE
Set Q to Q.Left
ENDIF
ELSE
IF( Q.Right is null)
Set Q.Right to P
Set Inserted to True
ELSE
Set Q to Q.Right
ENDIF
ENDIF
ENDWHILE
Removing an Element from a Binary Search Tree
This operation is a little more complex. First we must find the node to be removed. Let P be a node pointer that starts at the root and traverses the tree until it finds the node to be removed. We need to consider three cases.
First case: The node pointed to by P has no children. This means that P points to a leaf node and is easy to delete. We just set P’s parent pointer to null and we are done. Of course there is an implementation issue: If P points to the node to be deleted, how do we access the parent of P? One solution to is problem is to use a second pointer Q. When P traverses the tree looking for the node to be deleted, Q is set to P before moving P. In this way, Q always points to the parent of the node that P points to.
Second case: The node pointed to by P has one child. In this case, we just set P’s parent to point to P’s child.
Third case: P has two children. First find the node in the tree that is the next largest. To do this let T be a node pointer that is initialized to P’s right child. As long as T.Left is not null, let T = T.Left. Now swap the values in the nodes pointed to by P and T and delete the node pointed to by T.
Example In the tree above, with 21 and 44 added, remove 32 and 42.
One difficulty of a BST is that frequent insertions and deletions tend to make the tree out of balance. The search time for an out-of-balance BST degenerates to that of a linked list. Two approaches to this are AVL trees and Red-Black trees.