Stacks
From
(→Implementation of Stacks) |
(→Implementation of Stacks) |
||
| Line 23: | Line 23: | ||
With an array, we need an isFull() operation. There is normally an index called top, which is initialized to -1. Given this, the push() operation is | With an array, we need an isFull() operation. There is normally an index called top, which is initialized to -1. Given this, the push() operation is | ||
<pre> | <pre> | ||
| - | FUNCTION push() | + | FUNCTION push( ) |
| - | IF not isFull() | + | IF not isFull( ) |
Let top = top + 1 | Let top = top + 1 | ||
Let Stack[ top ] = data | Let Stack[ top ] = data | ||
| Line 32: | Line 32: | ||
The pop() operations can then be implemented with | The pop() operations can then be implemented with | ||
<pre> | <pre> | ||
| - | FUNCTION pop() | + | FUNCTION pop( ) |
| - | IF not isEmpty( | + | IF not isEmpty( ) |
LET top = top - 1 | LET top = top - 1 | ||
return( stack[ top ] ) | return( stack[ top ] ) | ||
| Line 42: | Line 42: | ||
</pre> | </pre> | ||
The isFull() operation is | The isFull() operation is | ||
| - | <pre> | + | <pre> |
| + | FUNCTION isFull( ) | ||
| + | IF top equals N - 1 THEN | ||
| + | return TRUE | ||
| + | ELSE | ||
| + | return FALSE | ||
| + | ENDIF | ||
| + | ENDFUNCTION | ||
| + | </pre> | ||
And the isEmpty() operation is | And the isEmpty() operation is | ||
<pre>return( top == -1 )</pre> | <pre>return( top == -1 )</pre> | ||
Revision as of 03:57, 1 April 2009
The Stack ADT is a collection of homogeneous data that organizes its entries according to the order in which they were added. The organization is called LIFO or Last In, First Out (Sometimes called FILO). In the ADT Stack, there is one access point called the top of the stack, and only the item at the top, which is the most recently added item, is visible. The normal operations that can be performed on a stack are: push(), pop(), peek(), and isEmpty(). Sometimes there will be an operation called isFull().
Intuitively, a stack is like a pile of plates where we can only remove a plate from the top and can only add a new plate on the top. In computer science we commonly place numbers on a stack, or perhaps place records on the stack.
Behavior of Stacks
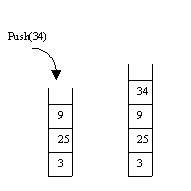
The Push operation places a new data item on top of the stack. Pop removes the top item and sends it back via the parameter. Finally, the Empty operation tells us whether or not the stack object is empty. Here are a picture of a small stack of integers and another picture of the stack after 34 has been pushed:
Implementation of Stacks
One of the many uses of a stack is to reverse data. Consider a singly linked list of numbers that is kept in order from smallest (at the head) to the largest (at the rear). What if I wanted to print out the numbers in order from largest to smallest? Implementation. A stack is usually implemented in one of two ways: either using an array or a linked list.
With an array, we need an isFull() operation. There is normally an index called top, which is initialized to -1. Given this, the push() operation is
FUNCTION push( )
IF not isFull( )
Let top = top + 1
Let Stack[ top ] = data
ENDIF
ENDFUNCTION
The pop() operations can then be implemented with
FUNCTION pop( )
IF not isEmpty( )
LET top = top - 1
return( stack[ top ] )
ELSE
return null
ENDIF
ENDFUNCTION
The isFull() operation is
FUNCTION isFull( )
IF top equals N - 1 THEN
return TRUE
ELSE
return FALSE
ENDIF
ENDFUNCTION
And the isEmpty() operation is
return( top == -1 )
When a stack is implemented as a linked list, we do not usually need the isFull() operations, but the isEmpty() operation is the same as that of the list. The normal way to implement the stack is to add and remove nodes from the head of the list. Note that if we do this, we do not need to use a rear pointer for the list.
Note also that a stack is an efficient data structure as all operations are constant. The array based stack wastes space that the linked list does not.
