Computability and Complexity
From
Contents |
Computability theory
Part of the theory of computation dealing with which problems are solvable by algorithms (equivalently, by Turing machines), with various restrictions and extensions. Computability theory addresses four main questions:
- What problems can Turing machines solve?
- What other systems are equivalent to Turing machines?
- What problems require more powerful machines?
- What problems can be solved by less powerful machines?
Not all problems can be solved. An undecidable problem is one that cannot be solved by any algorithm, even given unbounded time and memory. Many undecidable problems are known. For example, the Entscheidungsproblem (German for "decision problem") is this: given a statement in first-order predicate calculus, decide whether it is universally valid. Church and Turing independently proved this is undecidable. The halting problem is: given a program and inputs for it, decide whether it will run forever or will eventually halt. Turing proved this is also undecidable. A computable number is a real number which can be approximated to any arbitrary degree of accuracy by an algorithm. Turing proved that almost all numbers are uncomputable.
Practical implications of Computability and Complexity
The idea here is to present some basic computer science theory that has practical implications. The areas discussed include unsolvable problems, exponential running times, the classification of problems, and proofs of program correctness.
The General Halting Problem
The question: Is there an algorithm which when given any program and any set of input data for the program, can decide in advance whether or not the program will run forever (i.e. never halt)?
Theorem: There can be no such decision algorithm (assuming Church's thesis, which in practice everyone accepts and which says that every function that is computable by some sort of algorithm is computable by a Turing machine).
Practical Conclusion: There are definite limits to what our computer programs can do. There may be no algorithms possible to do some desirable things. In other words, some problems are simply unsolvable.
Exponential Running Times
We have already learned that exponential running times are "horrible" and polynomial running times are fairly reasonable. It appears that some problems may have only exponential running time solutions. This means that except for extremely simple cases of these problems they cannot be solved in a reasonable amount of time on even the fastest of computers (and even though a correct computer program exists to calculate the solutions).
Example: The Traveling Salesperson Problem (TSP)
The problem: Given n interconnected cities and the distances between them, find the lowest-distance tour of all the cities, starting and ending with a given city. A tour never revisits a city (other than the starting city, which we obviously visit twice).
All known solutions of this problem require exponential running time. Thus as n increases, the running time increases at least as fast as some 2^n function (which may have a positive constant in front of the 2^n). When we have n = 10 cities, the problem is solvable in a reasonable amount of time. However, it has been calculated that by the time we reach just n = 30 cities, it would take about 84 trillion centuries on a supercomputer that could do a billion operations per second!
Other problems that we try to solve by computer may also turn out to require exponential running times and hence only be solvable in a reasonable amount of time for very small values of n.
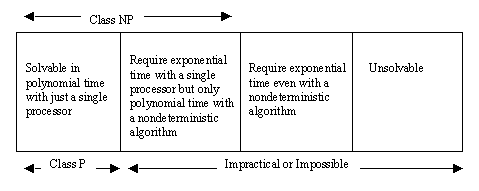
A nondeterministic algorithm is one that assigns different cases of a problem to different processors. It assumes that as many processors are available as needed (an assumption that is not true of real parallel processing machines since they have a definite fixed number of processors).
- Class P: Problems solvable in polynomial time on a single CPU Class
- NP: Problems solvable in polynomial time with a nondeterministic algorithm
Note that P is a subset of NP. It is thought that P and NP are not equal, so that NP is larger than P, though no one has been able to prove this. For example, the TSP is in NP, but as far as we know is not in P. A problem is NP-complete provided it is in NP and every problem in NP can be reduced to this problem in polynomial time. The TSP has been shown to be NP-complete. This means that if anyone ever does find a polynomial-time solution to the TSP, then all problems in NP will be solvable in polynomial time (hence proving that P = NP after all).
Finally, recall that the General Halting Problem is unsolvable. It, then, gives an example of a problem in the final box of our problem classification scheme.
Conclusion: There are many nasty problems (those not in P) that computers cannot solve at all or cannot solve in a reasonable length of time.