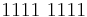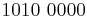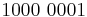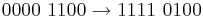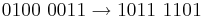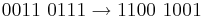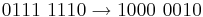A-level Computing/Processing and Programming Techniques/Data Representation in Computers/Answers
From
Revision as of 11:26, 22 June 2007 by 212.135.1.186 (Talk)
Hexadecimal
Help is available here
- Convert the following bases to their equivalent hexadecimal values
- 816
- A16
- 1016
- 116
- 516
- F16
- AB16
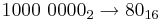
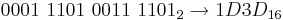
- AF0BE16
- Convert the following hexadecimal values to the given base
- 1410
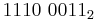
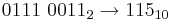
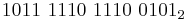
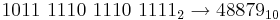
- 42617416
- Hexadecimal numbers are easier for humans to read, understand and remember.
Negative Binary Numbers
Help is available here
- What are the denary values of the following twos complement numbers?
- 27
- − 1
- 125
- − 103
- − 72
- Convert the following numbers into negative numbers written in binary
- Convert the following hexadecimal values to the given base
- − 3
- − 12
- Find the answers to the following sums in binary, show your working - not yet finished beyond here (YR 12 please complete!!)
- 0110 1100 - 0000 0111 = 01100101
- 0001 1111 - 0001 0011
- 0111 0111 - 0101 1011
- 23 (hex) - 1F (hex)
- 0001 0010 - 1111 1101
Binary Fractions
Help is available here
- What are the values of the following numbers where there are 4 numbers before the decimal point?
- 0011.1000
- 0101.0111
- 0110.1100
- EF
- 1001.0011
- 1100.1101 (note: this number is a two's complement number)
- Using 1 byte for each number, with a fixed unsigned decimal point between bits 4 and 5, convert the following denary/decimal numbers into binary or get as close as you can
- 0001.1000
- 1000.1100
- 1001.0011
- 0000.1001
- 1101.1001 (as close as you can get)
- What are the values of the following 16 bit floating point numbers, where the exponent is 6 bits
- 0111 0100 1100 1110
- 0110 0000 0011 1010
- 1011 1100 0100 0001
- 1110 0000 0011 1101
- Normalise the following 16 bit floating point numbers, where the exponent is 6 bits
- 0011 0000 0000 0001
- 0001 1100 0000 1110
- 1101 0110 0100 0010
- 1111 0111 1111 1001