Data Structures/Min and Max Heaps

From

Contents 1 Min and Max Heaps 1.1 Compute the extreme value 1.2 Removing the Extreme Value 1.3 Inserting a value into the heap 1.4 TODO

Min and Max Heaps

A heap is an efficient semi-ordered data structure for storing a collection of orderable data. A min-heap supports two operations:

  INSERT(heap, element)
  element REMOVE_MIN(heap)

(we discuss min-heaps, but there's no real difference between min and max heaps, except how the comparison is interpreted.)

This chapter will refer exclusively to binary heaps, although different types of heaps exist. The term binary heap and heap are interchangeable in most cases. A heap can be thought of as a tree with parent and child. The main difference between a heap and a binary tree is the heap property. In order for a data structure to be considered a heap, it must satisfy the following condition (heap property):

If A and B are elements in the heap and B is a child of A, then key(A) ≤ key(B).

(This property applies for a min-heap. A max heap would have the comparison reversed). What this tells us is that the minimum key will always remain at the top and greater values will be below it. Due to this fact, heaps are used to implement priority queues which allows quick access to the item with the most priority. Here's an example of a min-heap:

A heap is implemented using an array that is indexed from 1 to N, where N is the number of elements in the heap.

At any time, the heap must satisfy the heap property

  array[n] <= array[2*n]

and

  array[n] <= array[2*n+1]

whenever the indices are in the arrays bounds.

Compute the extreme value

We will prove that array[1] is the minimum element in the heap. We prove it by seeing a contradiction if some other element is less than the first element. Suppose array[i] is the first instance of the minimum, with array[j] > array[i] for all j < i, and 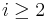. But by the heap invariant array, array[floor(i / 2)] < = array[i]: this is a contradiction.

Therefore, it is easy to compute MIN(heap):

  MIN(heap)
     return heap.array[1];

Removing the Extreme Value

To remove the minimum element, we must adjust the heap to fill heap.array[1]. This process is called percolation. Basically, we move the hole from node i to either node 2i or 2i + 1. If we pick the minimum of these two, the heap invariant will be maintained; suppose array[2i] < array[2i + 1]. Then array[2i] will be moved to array[i], leaving a hole at 2i, but after the move array[i] < array[2i + 1], so the heap invariant is maintained. In some cases, 2i + 1 will exceed the array bounds, and we are forced to percolate 2i. In other cases, 2i is also outside the bounds: in that case, we are done.

Therefore, here is the remove algorithm:

#define LEFT(i) (2*i + 1)

#define RIGHT(i) (2*i + 2)  

REMOVE_MIN(heap)
{  

        savemin=arr[0];
        arr[0]=arr[--heapsize];
        i=0;
        while(i<heapsize){
            minidx=i;
            if(LEFT(i)<heapsize && arr[LEFT(i)] < arr[i])
                minidx=LEFT(i);
            if(RIGHT(i)<heapsize && arr[RIGHT(i)] < arr[minidx]) 
                minidx=RIGHT(i);
            if(mindx!=i){
                swap(arr[i],arr[minidx]);
                i=minidx;            
            }
            else 
                break;
        }
}

Why this works ?

   If there is only 1 element ,heapsize becomes 0, nothing in the array is valid.
   If there are 2 elements , one min and other max, you replace min with max.
   If there are 3 or more elements say n, you replace 0th element with n-1th element. 
   The heap property is destroyed. Choose the 2 childs of root and check which is the minimum.
   Choose the minimum among them , swap it . Now subtree with swapped child is looses heap property.
   If no violations break.

Inserting a value into the heap

A similar strategy exists for INSERT: just append the element to the array, then fixup the heap-invariants by swapping. For example if we just appended element N, then the only invariant violation possible involves that element, in particular if array[floor(N / 2)] > array[N], then those two elements must be swapped and now the only invariant violation possible is between

 array[floor(N/4)]  and  array[floor(N/2)]

we continue iterating until N=1 or until the invariant is satisfied.

INSERT(heap, element)
   append(heap.array, element)
   i = heap.array.length
   while (i > 1)
     {
       if (heap.array[i/2] <= heap.array[i])
         break;
       swap(heap.array[i/2], heap.array[i]);
       i /= 2;
     }

TODO

 Merge-heap: it would take two max/min heap and merge them and return a single heap. O(n) time.
 Make-heap: it would also be nice to describe the O(n) make-heap operation
 Heap sort: the structure can actually be used to efficiently sort arrays
 Treaps: heaps where elements can be deleted by name

---

Edit this chapter