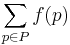Common Graph Algorithms
From
(Created page with '== Graph depth-first traversal == Same algorithm as with the tree ADT, but you have to check for nodes that have already been visited, usually by marking the node somehow. Detai...') |
(→Shortest Path algorithms) |
||
| Line 16: | Line 16: | ||
== Shortest Path algorithms == | == Shortest Path algorithms == | ||
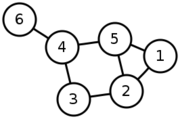
| - | + | [[Image:6n-graf.svg|thumb|A graph with 6 vertices and 7 edges]] | |
| - | < | + | In [[graph theory]], the '''shortest path problem''' is the problem of finding a [[path (graph theory)|path]] between two [[vertex (graph theory)|vertices]] (or nodes) such that the sum of the [[Glossary of graph theory#Weighted graphs and networks|weights]] of its constituent edges is minimized. An example is finding the quickest way to get from one location to another on a road map; in this case, the vertices represent locations and the edges represent segments of road and are weighted by the time needed to travel that segment. |
| + | |||
| + | Formally, given a weighted graph (that is, a set ''V'' of vertices, a set ''E'' of edges, and a [[real number|real]]-valued weight function ''f'' : ''E'' → '''R'''), and one element ''v'' of ''V'', find a path ''P'' from ''v'' to each ''v' '' of ''V'' so that | ||
| + | |||
| + | :<math>\sum_{p\in P} f(p)</math> | ||
| + | |||
| + | is minimal among all paths connecting ''v'' to ''v' ''. | ||
| + | |||
| + | The problem is also sometimes called the '''single-pair shortest path problem''', to distinguish it from the following generalizations: | ||
| + | * The '''single-source shortest path problem''', in which we have to find shortest paths from a source vertex ''v'' to all other vertices in the graph. | ||
| + | * The '''single-destination shortest path problem''', in which we have to find shortest paths from all vertices in the graph to a single destination vertex ''v''. This can be reduced to the single-source shortest path problem by reversing the edges in the graph. | ||
| + | * The '''all-pairs shortest path problem''', in which we have to find shortest paths between every pair of vertices ''v'', ''v' '' in the graph. | ||
| + | |||
| + | These generalizations have significantly more efficient algorithms than the simplistic approach of running a single-pair shortest path algorithm on all relevant pairs of vertices. | ||
| + | |||
| + | ==Algorithms== | ||
| + | The most important algorithms for solving this problem are: | ||
| + | * [[Dijkstra's algorithm]] solves the single-pair, single-source, and single-destination shortest path problems. | ||
| + | * [[Bellman-Ford algorithm]] solves single source problem if edge weights may be negative. | ||
| + | * [[A* search algorithm]] solves for single pair shortest path using heuristics to try to speed up the search. | ||
| + | * [[Floyd-Warshall algorithm]] solves all pairs shortest paths. | ||
| + | * [[Johnson's algorithm]] solves all pairs shortest paths, and may be faster than Floyd-Warshall on [[sparse graph]]s. | ||
| + | * [[Perturbation theory]] finds (at worst) the locally shortest path. | ||
| + | |||
| + | ==Applications== | ||
| + | Shortest path algorithms are applied to automatically find directions between physical locations, such as driving directions on [[web mapping]] websites like [[Mapquest]] or [[Google Maps]]. | ||
| + | |||
| + | If one represents a nondeterministic [[abstract machine]] as a graph where vertices describe states and edges describe possible transitions, shortest path algorithms can be used to find an optimal sequence of choices to reach a certain goal state, or to establish lower bounds on the time needed to reach a given state. For example, if vertices represents the states of a puzzle like a [[Rubik's Cube]] and each directed edge corresponds to a single move or turn, shortest path algorithms can be used to find a solution that uses the minimum possible number of moves. | ||
| + | |||
| + | In a networking or telecommunications mindset, this shortest path problem is sometimes called the min-delay path problem and usually tied with a [[widest path problem]]. For example, the algorithm may seek the shortest (min-delay) widest path, or widest shortest (min-delay) path. | ||
| + | |||
| + | A more lighthearted application is the games of "[[six degrees of separation]]" that try to find the shortest path in graphs like movie stars appearing in the same film. | ||
| + | |||
| + | Other applications include "[[operations research]], plant and facility layout, [[robotics]], [[transportation]], and [[Very-large-scale integration|VLSI]] design".<ref>Danny Z. Chen. Developing Algorithms and Software for Geometric Path Planning Problems. ''ACM Computing Surveys'' 28A(4), December 1996.</ref> | ||
Revision as of 19:36, 29 March 2009
Contents |
Graph depth-first traversal
Same algorithm as with the tree ADT, but you have to check for nodes that have already been visited, usually by marking the node somehow.
Details to be written..
Graph breadth-first traversal
Same algorithm as with the tree ADT, but you have to check for nodes that have already been visited, usually by marking the node somehow.
Details to be written..
Minimum Spanning Tree algorithms
To be written...
Shortest Path algorithms
In graph theory, the shortest path problem is the problem of finding a path between two vertices (or nodes) such that the sum of the weights of its constituent edges is minimized. An example is finding the quickest way to get from one location to another on a road map; in this case, the vertices represent locations and the edges represent segments of road and are weighted by the time needed to travel that segment.
Formally, given a weighted graph (that is, a set V of vertices, a set E of edges, and a real-valued weight function f : E → R), and one element v of V, find a path P from v to each v' of V so that
is minimal among all paths connecting v to v' .
The problem is also sometimes called the single-pair shortest path problem, to distinguish it from the following generalizations:
- The single-source shortest path problem, in which we have to find shortest paths from a source vertex v to all other vertices in the graph.
- The single-destination shortest path problem, in which we have to find shortest paths from all vertices in the graph to a single destination vertex v. This can be reduced to the single-source shortest path problem by reversing the edges in the graph.
- The all-pairs shortest path problem, in which we have to find shortest paths between every pair of vertices v, v' in the graph.
These generalizations have significantly more efficient algorithms than the simplistic approach of running a single-pair shortest path algorithm on all relevant pairs of vertices.
Algorithms
The most important algorithms for solving this problem are:
- Dijkstra's algorithm solves the single-pair, single-source, and single-destination shortest path problems.
- Bellman-Ford algorithm solves single source problem if edge weights may be negative.
- A* search algorithm solves for single pair shortest path using heuristics to try to speed up the search.
- Floyd-Warshall algorithm solves all pairs shortest paths.
- Johnson's algorithm solves all pairs shortest paths, and may be faster than Floyd-Warshall on sparse graphs.
- Perturbation theory finds (at worst) the locally shortest path.
Applications
Shortest path algorithms are applied to automatically find directions between physical locations, such as driving directions on web mapping websites like Mapquest or Google Maps.
If one represents a nondeterministic abstract machine as a graph where vertices describe states and edges describe possible transitions, shortest path algorithms can be used to find an optimal sequence of choices to reach a certain goal state, or to establish lower bounds on the time needed to reach a given state. For example, if vertices represents the states of a puzzle like a Rubik's Cube and each directed edge corresponds to a single move or turn, shortest path algorithms can be used to find a solution that uses the minimum possible number of moves.
In a networking or telecommunications mindset, this shortest path problem is sometimes called the min-delay path problem and usually tied with a widest path problem. For example, the algorithm may seek the shortest (min-delay) widest path, or widest shortest (min-delay) path.
A more lighthearted application is the games of "six degrees of separation" that try to find the shortest path in graphs like movie stars appearing in the same film.
Other applications include "operations research, plant and facility layout, robotics, transportation, and VLSI design".[1]