Binary Trees

From

A binary tree is is a tree ADT that is restricted to having at most 2 children in each node contained in the tree. As computers generally operated on digital/binary logic, binary trees are very natural and efficient structures. They are useful both as a means of storing and organizing data, and as a means of representing a solution to a problem.

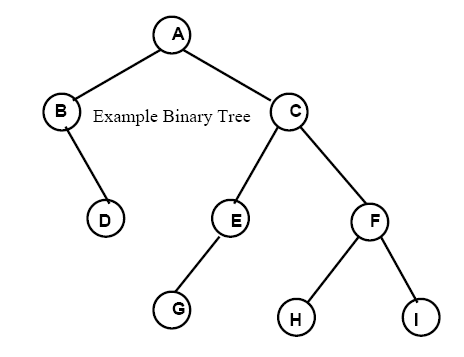
Here is an example binary tree:

Implementation of binary trees

A binary tree can be implemented in two basic ways. One way is a pointer based implementation—using dynamic memory—and the other way is an array based implementation—using static memory.

In a pointer based implementation, a tree node normally consists of three fields. They are usually called Data, Left, and Right. The Data field holds what ever information is to be represented by the tree, while the Left and Right fields are pointers to tree nodes. The links are normally one way: we can go from a parent to a child but not the other way.

In an array based implementation, the root of the tree is stored in position 0. For any node in position r, the left child is found in position 2r + 1 and the right child is found in position 2r + 2. One advantage of an array based implementation is that it is easy to go from a child to a parent: if the child is in location r and r > 0, then (r-1)/2, if r is odd, gives the location of the parent, and (r-2)/2, if r is even, gives the location of the parent. Also, if r > 0 and r is even, then r – 1 is the location of the sibling. And if r > 0 and r is odd, r + 1 is the location of the sibling.

Traversing a Binary Tree

Traversing a tree means to move systematically from node to node until all nodes have been covered or visited. There are several different algorithms for traversing a binary tree. In these algorithms we use a generic term called visit to indicate the operation that is being performed at each node. We also assume that we have a means of marking a node once it is visited. We may think of this as leaving a trail of bread crumbs or painting the node blue or leaving a post-it note that we were here.

The algorithms fall into two basic styles: breadth-first or depth-first traversals. The depthfirst traversals are called in-order, pre-order, post-order. What distinguishes a breadthfirst traversal from a depth-first traversal is the data structure that is used to hold the nodes we are waiting to visit. A breadth-first traversal uses a queue to hold the nodes and a depthfirst traversal uses a stack to hold the nodes we are waiting to visit.

We will consider the depth-first traversals first.

Depth-first traversals are almost always expressed in a recursive algorithm because it is very easy to describe the algorithm.

In-Order Traversal( Node N )
    IF N is not NULL
        In-Order Traversal( N.left )
        Visit( N )
        In-Order Traversal( N.right )
    ENDIF

In-Order Traversal of the example tree above: B, D, A, G. E, C, H, F, I

Pre-Order Traversal( Node N )
    IF N is not NULL
        Visit( N )
        Pre-Order Traversal( N.left )
        Pre-Order Traversal( N.right )
    ENDIF

Pre-Order Traversal of the example tree above: A, B, D, C, E, G, F, H, I

Post-Order Traversal( Node N )
    IF N is not NULL
        Post-Order Traversal( N.left )
        Post-Order Traversal( N.right )
        Visit( N )
    ENDIF

Post-Order Traversal of the example tree above: D, B, G, E, H, I, F, C, A

A Breadth-First Traversal has the following algorithm

Let Q be a queue that holds tree nodes and let P be a pointer to tree nodes.
<br/>
Enqueue the root of the tree.
<br/>
WHILE the queue is not empty do the following
    Dequeue a node and assign it to P
    Visit the node pointed to by P
    IF the node pointed to by P has a left child 
        enqueue the left child
    ENDIF
    IF the node pointed to by P has a right child 
        enqueue the right child
    ENDIF
ENDWHILE

Using this algorithm we get: A, B, C, D, E, F, G, H, I. A breadth-first traversal is often called a level-order traversal.