Computability and Complexity
From
| Begin | ↑ Contents: CS2 | Asymptotic Measures → |
The theory of computation is the branch of computer science that deals with whether and how efficiently problems can be solved on a model of computation, using an algorithm. The field is divided into two major branches: computability theory and complexity theory, but both branches deal with formal models of computation.
In order to perform a rigorous study of computation, computer scientists work with a mathematical abstraction of computers called a model of computation. There are several models in use, but the most commonly examined is the Turing machine. A Turing machine can be thought of as a desktop PC with a potentially infinite memory capacity, though it can only access this memory in small discrete chunks. Computer scientists study the Turing machine because it is simple to formulate, can be analyzed and used to prove results, and because it represents what many consider the most powerful possible "reasonable" model of computation. It might seem that the potentially infinite memory capacity is an unrealizable attribute, but any decidable problem solved by a Turing machine will always require only a finite amount of memory. So in principle, any problem that can be solved (decided) by a Turing machine can be solved by a computer that has a bounded amount of memory.
Contents |
Computability theory
Computability theory deals primarily with the question of whether a problem is solvable at all on a computer. The statement that the halting problem cannot be solved by a Turing machine is one of the most important results in computability theory, as it is an example of a concrete problem that is both easy to formulate and impossible to solve using a Turing machine. Much of computability theory builds on the halting problem result.
Thus Computability Theory is the part of the Theory of Computation dealing with which problems are solvable by algorithms (equivalently, by Turing machines), with various restrictions and extensions. Computability theory addresses four main questions:
- What problems can Turing machines solve?
- What other systems are equivalent to Turing machines?
- What problems require more powerful machines?
- What problems can be solved by less powerful machines?
Not all problems can be solved. An undecidable problem is one that cannot be solved by any algorithm, even given unbounded time and memory. Many undecidable problems are known. For example, the Entscheidungsproblem (German for "decision problem") is this: given a statement in first-order predicate calculus, decide whether it is universally valid. Church and Turing independently proved this is undecidable. The halting problem is: given a program and inputs for it, decide whether it will run forever or will eventually halt. Turing proved this is also undecidable. A computable number is a real number which can be approximated to any arbitrary degree of accuracy by an algorithm. Turing proved that almost all numbers are uncomputable.
Complexity theory
An engineer might ask "As the size of the input to an algorithm increases, by what factor does the running time and memory requirements increase? And what are the implications of that?" In other words, complexity theory, among other things, investigates the scalability of computational problems and algorithms. In particular, it places practical limits on what computers can and cannot reasonably accomplish.
A problem is a collection of related questions, where each question is a finite string, not enumerated but written in an algebra called Big O notation, where the actual amount of resources uses numbers only to represent orders of magnitude and not the exact resources used by a particular machine.
So, Complexity Theory is part of the theory of computation dealing with the resources required during computation to solve a given problem. The most common resources are time (how many steps does it take to solve a problem) and space (how much memory does it take to solve a problem). Other resources can also be considered, such as how many parallel processors are needed to solve a problem in parallel. Complexity theory differs from computability theory, which deals with whether a problem can be solved at all, regardless of the resources required.
A single "problem" is an entire set of related questions, where each question is a finite-length string. For example, the problem FACTORIZE is: given an integer written in binary, return all of the prime factors of that number. A particular question is called an instance. For example, "give the factors of the number 15" is one instance of the FACTORIZE problem.
The time complexity of a problem is the number of steps that it takes to solve an instance of the problem, as a function of the size of the input, (usually measured in bits) using the most efficient algorithm. To understand this intuitively, consider the example of an instance that is n bits long that can be solved in n² steps. In this example we say the problem has a time complexity of n². Of course, the exact number of steps will depend on exactly what machine or language is being used. To avoid that problem, we generally use Big O notation. If a problem has time complexity O(n²) on one typical computer, then it will also have complexity O(n²) on most other computers, so this notation allows us to generalize away from the details of a particular computer.
Example: Mowing grass has linear complexity because it takes double the time to mow double the area. However, looking up something in a dictionary has only logarithmic complexity because for a double sized dictionary you have to open it only one time more (e.g. exactly in the middle - then the problem is reduced to the half).
Practical implications of Computability and Complexity
The idea here is to present some basic computer science theory that has practical implications. The areas discussed include unsolvable problems, exponential running times, and the classification of problems.
The General Halting Problem
The question: Is there an algorithm which when given any program and any set of input data for the program, can decide in advance whether or not the program will run forever (i.e. never halt)?
Theorem: There can be no such decision algorithm (assuming Church's thesis, which in practice everyone accepts and which says that every function that is computable by some sort of algorithm is computable by a Turing machine).
Practical Conclusion: There are definite limits to what our computer programs can do. There may be no algorithms possible to do some desirable things. In other words, some problems are simply unsolvable.
Exponential Running Times
We have already learned that exponential running times are "horrible" and polynomial running times are fairly reasonable. It appears that some problems may have only exponential running time solutions. This means that except for extremely simple cases of these problems they cannot be solved in a reasonable amount of time on even the fastest of computers (and even though a correct computer program exists to calculate the solutions).
Example: The Traveling Salesperson Problem (TSP)
The problem: Given n interconnected cities and the distances between them, find the lowest-distance tour of all the cities, starting and ending with a given city. A tour never revisits a city (other than the starting city, which we obviously visit twice).
All known solutions of this problem require exponential running time. Thus as n increases, the running time increases at least as fast as some 2^n function (which may have a positive constant in front of the 2^n). When we have n = 10 cities, the problem is solvable in a reasonable amount of time. However, it has been calculated that by the time we reach just n = 30 cities, it would take about 84 trillion centuries on a supercomputer that could do a billion operations per second!
Other problems that we try to solve by computer may also turn out to require exponential running times and hence only be solvable in a reasonable amount of time for very small values of n.
A nondeterministic algorithm is one that assigns different cases of a problem to different processors. It assumes that as many processors are available as needed (an assumption that is not true of real parallel processing machines since they have a definite fixed number of processors).
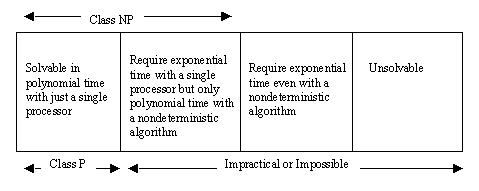
- Class P: Problems solvable in polynomial time on a single CPU Class
- NP: Problems solvable in polynomial time with a nondeterministic algorithm
Note that P is a subset of NP. It is thought that P and NP are not equal, so that NP is larger than P, though no one has been able to prove this. For example, the TSP is in NP, but as far as we know is not in P. A problem is NP-complete provided it is in NP and every problem in NP can be reduced to this problem in polynomial time. The TSP has been shown to be NP-complete. This means that if anyone ever does find a polynomial-time solution to the TSP, then all problems in NP will be solvable in polynomial time (hence proving that P = NP after all).
Finally, recall that the General Halting Problem is unsolvable. It, then, gives an example of a problem in the final box of our problem classification scheme.
Conclusion: There are many nasty problems (those not in P) that computers cannot solve at all or cannot solve in a reasonable length of time.
When is Efficiency Important?
Not every problem requires the most efficient solution available. For our purposes, the term efficient is concerned with the time and or space needed to perform the task. When either time or space is abundant and cheap, it may not be worth it to pay a programmer to spend a day or so working to make a program faster.
However, here are some cases where efficiency matters:
- When resources are limited, a change in algorithms could create great savings and allow limited machines (like cell phones, embedded systems, and sensor networks) to be stretched to the frontier of possibility.
- When the data is large a more efficient solution can mean the difference between a task finishing in two days versus two weeks. Examples include physics, genetics, web searches, massive online stores, and network traffic analysis.
- Real time applications: the term "real time applications" actually refers to computations that give time guarantees, versus meaning "fast." However, the quality can be increased further by choosing the appropriate algorithm.
- Computationally expensive jobs, like fluid dynamics, partial differential equations, VLSI design, and cryptanalysis can sometimes only be considered when the solution is found efficiently enough.
- When a subroutine is common and frequently used, time spent on a more efficient implementation can result in benefits for every application that uses the subroutine. Examples include sorting, searching, pseudorandom number generation, kernel operations (not to be confused with the operating system kernel), database queries, and graphics.
In short, it's important to save time when you do not have any time to spare.
When is efficiency unimportant? Examples of these cases include prototypes that are used only a few times, cases where the input is small, when simplicity and ease of maintenance is more important, when the area concerned is not the bottle neck, or when there's another process or area in the code that would benefit far more from efficient design and attention to the algorithm(s).
CS2: Data Structures
Theory of Computation - ADT Preliminaries
Linear ADTs - Tree ADTs - Graph ADTs - Unordered Collection ADTs