Primitive and Composite Structures
From
m (Protected "Primitive and Compound Structures" ([edit=autoconfirmed] (indefinite) [move=autoconfirmed] (indefinite))) |
(→Array Usage) |
||
| (20 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | + | <noinclude> | |
| + | {{CS2:BookNav|base=/|up=Contents: CS2|prev=Memory Allocation|next=Concept of an Element (Node)}} | ||
| + | </noinclude> | ||
| + | <br/> | ||
| - | + | All languages start with primitive elements such as characters, floating point and fixed point numbers. While these hold data and require memory to store, they are not normally considered data structures; they only represent singular data values. | |
| + | |||
| + | Most programming languages also provide array and record structures, these are often considered '''composite''' structures as they are usually composed of multiple primitive values. However, these are not considered data structures as they provide no real behavior other than memory access. So, we begin with a short look at both an array and a record. | ||
== Arrays == | == Arrays == | ||
| + | An array is a homogeneous collection of data that is stored sequentially in memory. Arrays use a memory oriented method of storing '''elements''' of indexed data. Elements of data are stored sequentially in blocks within the array. Each element is referenced by an '''index''', or subscript. | ||
| + | <br/><br/> | ||
| + | |||
| + | An array has fast random access because of this: Since the data is homogeneous, I know the size, in bytes, of each entry in the array. Since the storage is sequential, if I know the starting address of the array, it is easy to calculate the address of any slot. Most languages provide an array as a basic data type. Many languages also allow for multidimensional arrays. | ||
| + | <br/><br/> | ||
| + | |||
| + | The index is usually a number used to address an element in the array. For example, if you were storing information about each day in August, you would create an array with an index capable of addressing 31 values -- one for each day of the month. Indexing rules are language dependent, however most languages use either 0 or 1 as the first element of an array. | ||
| + | <br/><br/> | ||
| + | |||
| + | The concept of an array can be daunting to the uninitiated, but it is really quite simple. Think of a notebook with pages numbered 1 through 12. Each page may or may not contain information on it. The notebook is an ''array'' of pages. Each page is an ''element'' of the array 'notebook'. Programmatically, you would retrieve information from a page by referring to its number or ''subscript'', i.e., notebook(4) would refer to the contents of page 4 of the array notebook. | ||
| + | |||
| + | |||
| + | <center>[[Image:SimpleArray.png]]<br>''The notebook (array) contains 12 pages (elements)''</center> | ||
| + | |||
| + | |||
| + | Arrays can also be multidimensional - instead of accessing an element of a one-dimensional list, elements are accessed by two or more indices, as from a matrix or tensor. | ||
| + | |||
| + | Multidimensional arrays are as simple as our notebook example above. To envision a multidimensional array, think of a calendar. Each page of the calendar, 1 through 12, is an element, representing a month, which contains approximately 30 elements, which represent days. Each day may or may not have information in it. Programmatically then, calendar(4,15) would refer to the 4th month, 15th day. Thus we have a two-dimensional array. To envision a three-dimensional array, break each day up into 24 hours. Now calendar(4,15,9) would refer to 4th month, 15th day, 9th hour. | ||
| + | |||
| + | |||
| + | <center>[[Image:MultidimensionalArray.png]]<br>''A simple 6 element by 4 element array''</center> | ||
| + | |||
| + | <br> | ||
| + | Arrays guarantee '''constant''' time read and write access, <math>O(1)</math>, however many lookup operations (find_min, find_max, find_index) of an instance of an element are '''linear''' time, <math>O(n)</math>. Arrays are very efficient in most languages, as operations compute the address of an element via a simple formula based on the base address element of the array. | ||
| + | |||
| + | The implementation of arrays differ greatly between languages: some languages allow arrays to be resized automatically, or to even contain elements of differing types (such as Perl). Other languages are very strict and require the type and length information of an array to be known at run time (such as C). | ||
| + | |||
| + | Arrays typically map directly to contiguous storage locations within your computers memory and are therefore the "natural" storage structure for most higher level languages. | ||
| + | |||
| + | Simple linear arrays are the basis for most of the other data structures. Many languages do not allow you to allocate any structure except an array, everything else must be implemented on top of the array. The exception is the linked list, that is typically implemented as individually allocated objects, but it is possible to implement a linked list within an array. | ||
| + | |||
| + | ==== Type ==== | ||
| + | The array index needs to be of some type. Usually, the standard integer type of that language is used, but there are also languages such as Ada and Pascal which allow any discrete type as an array index. Scripting languages often allow any type as an index (associative array). | ||
| + | <br/><br/> | ||
| + | |||
| + | ==== Bounds ==== | ||
| + | The array index consists of a range of values with a lower bound and an upper bound. In some programming languages only the upper bound can be chosen while the lower bound is fixed to be either 0 (as in C, C++ and Java) or 1 (FORTRAN). In other programming languages (Ada, PL/I, Pascal) both the upper and lower bound can be freely chosen (even negative). | ||
| + | <br/><br/> | ||
| + | |||
| + | ==== Bounds check ==== | ||
| + | The third aspect of an array index is the check for valid ranges and what happens when an invalid index is accessed. This is a very important point since the majority of computer worms and computer viruses attack by using invalid array bounds. | ||
| + | <br/><br/> | ||
| + | === Array Usage === | ||
| + | We generally write arrays with a name, followed by the index in some brackets, square '[]' or round '()'. For example, <tt>august[3]</tt> is the method used in the C programming language to refer to a particular day in the month. | ||
| + | <br/><br/> | ||
| + | |||
| + | Because the C language starts the index at zero, <tt>august[3]</tt> is the 4th element in the array. <tt>august[0]</tt> actually refers to the first element of this array. Starting an index at zero is natural for computers, whose internal representations of numbers begin with zero, but for humans, this unnatural numbering system can lead to problems when accessing data in an array. When fetching an element in a language with zero-based indexes, keep in mind the ''true'' length of an array, lest you find yourself fetching the wrong data. This is the disadvantage of programming in languanges with fixed lower bounds, the programmer must always remember that "[0]" means "1st" and, when appropriate, add or subtract one from the index. Languages with variable lower bounds will take that burden off the programmer's shoulder. | ||
| + | <br/><br/> | ||
| + | |||
| + | We use indexes to store ''related'' data. If our C language array is called <tt>august</tt>, and we wish to store that we're going to the supermarket on the 1st, we can say, for example | ||
| + | |||
| + | august[0] = "Going to the shops today" | ||
| - | + | In this way, we can go through the indexes from 0 to 30 and get the related tasks for each day in <tt>august</tt>. | |
| + | <br/><br/> | ||
| - | + | === Address Calculation Example: === | |
| + | Given A[ 4, 3 ], which has 4 rows and 3 columns. Suppose this is an array of ints, so each slot in the array takes 4 bytes. If the array is stored in column major order beginning at address 100, then the memory layout is the following. | ||
(..need diagram..) | (..need diagram..) | ||
| Line 36: | Line 95: | ||
<br> | <br> | ||
| - | ==Records== | + | == Records and Structures == |
A record is a heterogeneous collection of data. The components of a record structure are usually referred to as fields. Many languages provide the ability to construct records. For example, a Java class that has no methods or has only accessor and mutator methods is a form of a record structure. In this case, the class instance variables would be the fields of the record. | A record is a heterogeneous collection of data. The components of a record structure are usually referred to as fields. Many languages provide the ability to construct records. For example, a Java class that has no methods or has only accessor and mutator methods is a form of a record structure. In this case, the class instance variables would be the fields of the record. | ||
| Line 42: | Line 101: | ||
<br> | <br> | ||
| - | + | ---- | |
| + | {{CS2/ChapNav}} | ||
| + | ---- | ||
| + | [[Category:CS2|{{SUBPAGENAME}}]] | ||
Current revision as of 22:14, 9 April 2009
| ← Memory Allocation | ↑ Contents: CS2 | Concept of an Element (Node) → |
All languages start with primitive elements such as characters, floating point and fixed point numbers. While these hold data and require memory to store, they are not normally considered data structures; they only represent singular data values.
Most programming languages also provide array and record structures, these are often considered composite structures as they are usually composed of multiple primitive values. However, these are not considered data structures as they provide no real behavior other than memory access. So, we begin with a short look at both an array and a record.
Contents |
Arrays
An array is a homogeneous collection of data that is stored sequentially in memory. Arrays use a memory oriented method of storing elements of indexed data. Elements of data are stored sequentially in blocks within the array. Each element is referenced by an index, or subscript.
An array has fast random access because of this: Since the data is homogeneous, I know the size, in bytes, of each entry in the array. Since the storage is sequential, if I know the starting address of the array, it is easy to calculate the address of any slot. Most languages provide an array as a basic data type. Many languages also allow for multidimensional arrays.
The index is usually a number used to address an element in the array. For example, if you were storing information about each day in August, you would create an array with an index capable of addressing 31 values -- one for each day of the month. Indexing rules are language dependent, however most languages use either 0 or 1 as the first element of an array.
The concept of an array can be daunting to the uninitiated, but it is really quite simple. Think of a notebook with pages numbered 1 through 12. Each page may or may not contain information on it. The notebook is an array of pages. Each page is an element of the array 'notebook'. Programmatically, you would retrieve information from a page by referring to its number or subscript, i.e., notebook(4) would refer to the contents of page 4 of the array notebook.
The notebook (array) contains 12 pages (elements)
Arrays can also be multidimensional - instead of accessing an element of a one-dimensional list, elements are accessed by two or more indices, as from a matrix or tensor.
Multidimensional arrays are as simple as our notebook example above. To envision a multidimensional array, think of a calendar. Each page of the calendar, 1 through 12, is an element, representing a month, which contains approximately 30 elements, which represent days. Each day may or may not have information in it. Programmatically then, calendar(4,15) would refer to the 4th month, 15th day. Thus we have a two-dimensional array. To envision a three-dimensional array, break each day up into 24 hours. Now calendar(4,15,9) would refer to 4th month, 15th day, 9th hour.
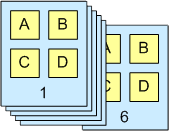
A simple 6 element by 4 element array
Arrays guarantee constant time read and write access, O(1), however many lookup operations (find_min, find_max, find_index) of an instance of an element are linear time, O(n). Arrays are very efficient in most languages, as operations compute the address of an element via a simple formula based on the base address element of the array.
The implementation of arrays differ greatly between languages: some languages allow arrays to be resized automatically, or to even contain elements of differing types (such as Perl). Other languages are very strict and require the type and length information of an array to be known at run time (such as C).
Arrays typically map directly to contiguous storage locations within your computers memory and are therefore the "natural" storage structure for most higher level languages.
Simple linear arrays are the basis for most of the other data structures. Many languages do not allow you to allocate any structure except an array, everything else must be implemented on top of the array. The exception is the linked list, that is typically implemented as individually allocated objects, but it is possible to implement a linked list within an array.
Type
The array index needs to be of some type. Usually, the standard integer type of that language is used, but there are also languages such as Ada and Pascal which allow any discrete type as an array index. Scripting languages often allow any type as an index (associative array).
Bounds
The array index consists of a range of values with a lower bound and an upper bound. In some programming languages only the upper bound can be chosen while the lower bound is fixed to be either 0 (as in C, C++ and Java) or 1 (FORTRAN). In other programming languages (Ada, PL/I, Pascal) both the upper and lower bound can be freely chosen (even negative).
Bounds check
The third aspect of an array index is the check for valid ranges and what happens when an invalid index is accessed. This is a very important point since the majority of computer worms and computer viruses attack by using invalid array bounds.
Array Usage
We generally write arrays with a name, followed by the index in some brackets, square '[]' or round '()'. For example, august[3] is the method used in the C programming language to refer to a particular day in the month.
Because the C language starts the index at zero, august[3] is the 4th element in the array. august[0] actually refers to the first element of this array. Starting an index at zero is natural for computers, whose internal representations of numbers begin with zero, but for humans, this unnatural numbering system can lead to problems when accessing data in an array. When fetching an element in a language with zero-based indexes, keep in mind the true length of an array, lest you find yourself fetching the wrong data. This is the disadvantage of programming in languanges with fixed lower bounds, the programmer must always remember that "[0]" means "1st" and, when appropriate, add or subtract one from the index. Languages with variable lower bounds will take that burden off the programmer's shoulder.
We use indexes to store related data. If our C language array is called august, and we wish to store that we're going to the supermarket on the 1st, we can say, for example
august[0] = "Going to the shops today"
In this way, we can go through the indexes from 0 to 30 and get the related tasks for each day in august.
Address Calculation Example:
Given A[ 4, 3 ], which has 4 rows and 3 columns. Suppose this is an array of ints, so each slot in the array takes 4 bytes. If the array is stored in column major order beginning at address 100, then the memory layout is the following.
(..need diagram..)
100 104 108 112 116 120 124 128 132 136 140 144
[0,0] [1,0] [2,0] [3,0] [0,1] [1,1] [2,1] [3,1] [0,2] [1,2] [2,2] [3,2]
To access location [2, 1] requires moving 1 column plus 2 more slots. Since a column is 4 slots or 16 bytes, then the address of [2, 1] is
100 + 1 column + 2 slots or 100 bytes + 4 slots * 4 bytes per slot + 2 slots * 4 bytes per slot or 100 bytes + 16 bytes + 8 bytes = 124 bytes.
However, to access the entire array we would typically write
for( int i = 0; i < 4; i ++ )
for( int j = 0; j < 3, j++ )
This gives the sequence: [0,0], [0,1], [0,2], [1,0], [1,1], [1,2], [2,1], [2,2], [3,0], [3,1], [3,2].
Is this a problem? Here is where the theoretical meets the practical. Consider a large array and paging.
Sparse arrays: A sparse array is one where more than half of it is empty. In this case is the array the best choice for the storage of the data?
Records and Structures
A record is a heterogeneous collection of data. The components of a record structure are usually referred to as fields. Many languages provide the ability to construct records. For example, a Java class that has no methods or has only accessor and mutator methods is a form of a record structure. In this case, the class instance variables would be the fields of the record.
Variant Records: A variant record is one where a single field can represent multiple data types, but only one type at a time. If you know what an overlay refers to in an operating system, a variant record is the same idea. That is, a variant record could have one field that might represent an int, or a double, or a boolean. It would have enough memory allocated to it to represent the biggest element, in this case a double, but only one component could be represented at a time.
CS2: Data Structures
Theory of Computation - ADT Preliminaries
Linear ADTs - Tree ADTs - Graph ADTs - Unordered Collection ADTs
