Stacks
From
(→A Stack Usage Example) |
(→Implementation of Stacks) |
||
| (6 intermediate revisions not shown) | |||
| Line 21: | Line 21: | ||
'''<code>Stack<item-type></code> Operations''' | '''<code>Stack<item-type></code> Operations''' | ||
<dl> | <dl> | ||
| - | <dt style="font-weight:normal"><code>'''push'''(<var>new-item</var> | + | <dt style="font-weight:normal"><code>'''push'''(<var>new-item</var>)</code> |
<dd>Adds an item onto the stack. | <dd>Adds an item onto the stack. | ||
| + | <dt style="font-weight:normal"><code>'''pop'''():item-type</code> | ||
| + | <dd>Removes the most-recently-pushed item from the stack. | ||
<dt style="font-weight:normal"><code>'''top'''():item-type</code> | <dt style="font-weight:normal"><code>'''top'''():item-type</code> | ||
<dd>Returns the last item pushed onto the stack. | <dd>Returns the last item pushed onto the stack. | ||
| - | <dt style="font-weight:normal"><code>''' | + | <dt style="font-weight:normal"><code>'''isFull'''():Boolean</code> |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<dd>True if no more items can be pushed. | <dd>True if no more items can be pushed. | ||
| - | <dt style="font-weight:normal"><code>''' | + | <dt style="font-weight:normal"><code>'''isEmpty'''():Boolean</code> |
| + | <dd>True if no more items can be popped and there is no top item. | ||
| + | <dt style="font-weight:normal"><code>'''getSize'''():Integer</code> | ||
<dd>Returns the number of elements on the stack. | <dd>Returns the number of elements on the stack. | ||
</dl> | </dl> | ||
| Line 45: | Line 45: | ||
Commonly, with an array implementation, we will use a 0 based array (an Array of size N has elements indexed from 0 to N - 1). We will need an isFull( ) operation as arrays are fixed size. There is normally an index called top, which is initialized to 0. Top commonly is the index of the next open slot in the array. Given this, we have the following definitions for the Stack ADT operations: | Commonly, with an array implementation, we will use a 0 based array (an Array of size N has elements indexed from 0 to N - 1). We will need an isFull( ) operation as arrays are fixed size. There is normally an index called top, which is initialized to 0. Top commonly is the index of the next open slot in the array. Given this, we have the following definitions for the Stack ADT operations: | ||
<br/><br/> | <br/><br/> | ||
| + | The push( ) operations is: | ||
| + | <pre> | ||
| + | FUNCTION push( ) | ||
| + | IF not isFull( ) | ||
| + | Let Stack[ top ] = data | ||
| + | Let top = top + 1 | ||
| + | ENDIF | ||
| + | ENDFUNCTION | ||
| + | </pre> | ||
| + | The pop( ) operation can then be implemented with | ||
| + | <pre> | ||
| + | FUNCTION pop( ) | ||
| + | IF not isEmpty( ) | ||
| + | LET top = top - 1 | ||
| + | return( stack[ top ] ) | ||
| + | ELSE | ||
| + | return null | ||
| + | ENDIF | ||
| + | ENDFUNCTION | ||
| + | </pre> | ||
| + | The top( ) operation can then be implemented with | ||
| + | <pre> | ||
| + | FUNCTION top( ) | ||
| + | IF not isEmpty( ) | ||
| + | return( stack[ top ] ) | ||
| + | ELSE | ||
| + | return null | ||
| + | ENDIF | ||
| + | ENDFUNCTION | ||
| + | </pre> | ||
The isFull( ) operation is | The isFull( ) operation is | ||
<pre> | <pre> | ||
| Line 65: | Line 95: | ||
ENDFUNCTION | ENDFUNCTION | ||
</pre> | </pre> | ||
| - | The | + | The getSize( ) operation is: |
<pre> | <pre> | ||
| - | FUNCTION | + | FUNCTION getSize( ) |
| - | + | return size | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
ENDFUNCTION | ENDFUNCTION | ||
</pre> | </pre> | ||
Current revision as of 21:02, 9 April 2009
| ← Linear ADTs | ↑ Contents: CS2 | Queues → |
The Stack ADT is a collection of homogeneous data that organizes its entries according to the order in which they were added. The organization is called LIFO or Last In, First Out (Sometimes called FILO). In the ADT Stack, there is one access point called the top of the stack, and only the item at the top, which is the most recently added item, is visible. The normal operations that can be performed on a stack are: push(), pop(), peek(), and isEmpty(). Sometimes there will be an operation called isFull().
Intuitively, a stack is like a pile of plates where we can only remove a plate from the top and can only add a new plate on the top. In computer science we commonly place numbers on a stack, or perhaps place records on the stack.
Contents |
Behavior of Stacks
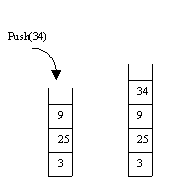
The Push operation places a new data item on top of the stack. Pop removes the top item and sends it back via the parameter. Finally, the Empty operation tells us whether or not the stack object is empty. Here are a picture of a small stack of integers and another picture of the stack after 34 has been pushed:
Stack<item-type> Operations
push(new-item)- Adds an item onto the stack.
pop():item-type- Removes the most-recently-pushed item from the stack.
top():item-type- Returns the last item pushed onto the stack.
isFull():Boolean- True if no more items can be pushed.
isEmpty():Boolean- True if no more items can be popped and there is no top item.
getSize():Integer- Returns the number of elements on the stack.
All operations except get-size() can be performed in O(1) time. get-size() runs in at worst O(N).
Implementation of Stacks
One of the many uses of a stack is to reverse data. Consider a singly linked list of numbers that is kept in order from smallest (at the head) to the largest (at the rear). What if I wanted to print out the numbers in order from largest to smallest? Implementation. A stack is usually implemented in one of two ways: either using an array or a linked list.
Commonly, with an array implementation, we will use a 0 based array (an Array of size N has elements indexed from 0 to N - 1). We will need an isFull( ) operation as arrays are fixed size. There is normally an index called top, which is initialized to 0. Top commonly is the index of the next open slot in the array. Given this, we have the following definitions for the Stack ADT operations:
The push( ) operations is:
FUNCTION push( )
IF not isFull( )
Let Stack[ top ] = data
Let top = top + 1
ENDIF
ENDFUNCTION
The pop( ) operation can then be implemented with
FUNCTION pop( )
IF not isEmpty( )
LET top = top - 1
return( stack[ top ] )
ELSE
return null
ENDIF
ENDFUNCTION
The top( ) operation can then be implemented with
FUNCTION top( )
IF not isEmpty( )
return( stack[ top ] )
ELSE
return null
ENDIF
ENDFUNCTION
The isFull( ) operation is
FUNCTION isFull( )
IF top equals N THEN
return TRUE
ELSE
return FALSE
ENDIF
ENDFUNCTION
The isEmpty( ) operation is:
FUNCTION isEmpty( )
IF top equals 0 THEN
return TRUE
ELSE
return FALSE
ENDIF
ENDFUNCTION
The getSize( ) operation is:
FUNCTION getSize( )
return size
ENDFUNCTION
When a stack is implemented as a linked list, we do not usually need the isFull() operations, but the isEmpty() operation is the same as that of the list. The normal way to implement the stack is to add and remove nodes from the head of the list. Note that if we do this, we do not need to use a rear pointer for the list.
Note also that a stack is an efficient data structure as all operations are constant. The array based stack wastes space that the linked list does not.
A Stack Usage Example
Evaluating a Postfix Expression:
You may be asking what a stack is good for, other than reversing a sequence of data items. One common application is to convert an infix expression to postfix. Another is to find the value of a postfix expression. We will not look at the conversion algorithm here, but we will examine the algorithm to evaluate a postfix expression.
First, let's explain the terminology. An infix expression is the type that we are used to in ordinary algebra, such as 3 + 9, which is an expression representing the sum of 3 and 9. Infix expressions place their (binary) operators between the two values to which they apply. In the above example, the addition operator was placed between the 3 and the 9.
A postfix expression, in contrast, places each operator after the two values to which it applies. (Post means "after", right?) The above expression would be 3 9 +, when rewritten in postfix.
Here are a few more examples in the following table. The infix form is shown on the left, and the postfix form is given on the right.
| Infix: | Postfix: |
| 16 / 2 | 16 2 / |
| (2 + 14) * 5 | 2 14 + 5 * |
| 2 + 14 * 5 | 2 14 5 * + |
| (6 - 2) * (5 + 4) | 6 2 - 5 4 + * |
Note that postfix expressions do not use parentheses for grouping; it is not needed! Infix sometimes requires parentheses to force a certain order of evaluation. For example, in the second example above, parentheses were needed to indicate that the addition should be done before the multiplication. Without the parentheses you get the third example, where the multiplication is done before the addition (using the precedence rules from ordinary arithmetic, or from C++, for that matter).
Arithmetic expressions like the above can of course be much longer. We could also allow other operators, such as ^ for exponentiation, or perhaps a unary minus. A sample infix expression that uses exponentiation is 4 ^ 2, which means 4 to the second power. A unary minus is sometimes used as in the infix expression -(4 + 2). A unary operator is one that is applied to a single value, as opposed to the typical binary operators, which are applied to two values. We will not consider unary operators or exponentiation further here.
The algorithm to evaluate a postfix expression works like this: Start with an empty stack of floats. Scan the postfix expression from left to right. Whenever you reach a number, push it onto the stack. Whenever you reach an operator (call it Op perhaps), pop two items, say First and Second, and then push the value obtained using Second Op First. When you reach the end of the postfix expression, pop a value from the stack. That value should be the correct answer, and the stack should now be empty. (If the stack is not empty, the expression was not a correct postfix expression.)
Let's look at the postfix expression evaluation algorithm by way of example. Consider the postfix expression 2 14 + 5 * that was mentioned above. We already know from its infix form, (2 + 14) * 5, that the value should be 16 * 5 = 80. The following sequence of pictures depicts the operation of the algorithm on this example. Read through the pictures from left to right.
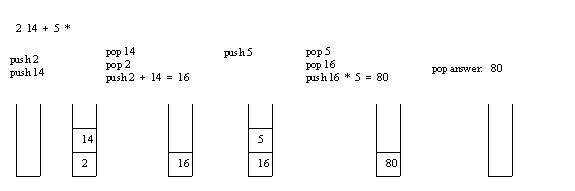
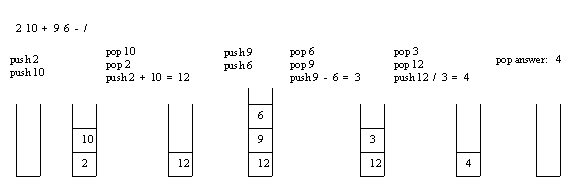
Let's evaluate another postfix expression, say 2 10 + 9 9 - /, which is (2 + 10) / (9 - 6) in infix. Clearly the value should work out to be 12 / 3 = 4. Trace through the algorithm by reading the following pictures from left to right.
When one reaches an operator in this algorithm, it is important to get the order right for the values to which it applies. The second item popped off should go in front of the operator, while the first one popped off goes after the operator. You can easily see that with subtraction and division the order does matter.
A good exercise for the reader is to develop a program that repeatedly evaluates postfix expressions. In fact, with enough work, it can be turned into a reasonable postfix calculator.
Related Links
CS2: Data Structures
Theory of Computation - ADT Preliminaries
Linear ADTs - Tree ADTs - Graph ADTs - Unordered Collection ADTs
