Hash Tables
From
(→Load Factor) |
(→Load Factor) |
||
| Line 85: | Line 85: | ||
'''last-come-first-served hashing''' and '''cuckoo hashing''' move existing keys around in the array to make room for the new key. This gives better maximum search times than the methods based on probing. | '''last-come-first-served hashing''' and '''cuckoo hashing''' move existing keys around in the array to make room for the new key. This gives better maximum search times than the methods based on probing. | ||
| - | == Load Factor == | + | === Load Factor === |
A critical influence on performance of an open addressing hash table is the ''load factor''; that is, the proportion of the slots in the array that are used. As the load factor increases towards 100%, the number of probes that may be required to find or insert a given key rises dramatically. Once the table becomes full, probing algorithms may even fail to terminate. Even with good hash functions, load factors are normally limited to 80%. A poor hash function can exhibit poor performance even at very low load factors by generating significant clustering. What causes hash functions to cluster is not well understood, and it is easy to unintentionally write a hash function which causes severe clustering. | A critical influence on performance of an open addressing hash table is the ''load factor''; that is, the proportion of the slots in the array that are used. As the load factor increases towards 100%, the number of probes that may be required to find or insert a given key rises dramatically. Once the table becomes full, probing algorithms may even fail to terminate. Even with good hash functions, load factors are normally limited to 80%. A poor hash function can exhibit poor performance even at very low load factors by generating significant clustering. What causes hash functions to cluster is not well understood, and it is easy to unintentionally write a hash function which causes severe clustering. | ||
<br/><br/> | <br/><br/> | ||
Revision as of 16:31, 19 April 2009
| ← Maps and Dictionaries | ↑ Contents: CS2 | End |
Hashing is called a Key to Address system. Objects (records) are stored in a table, and each object stored occupies a slot in the table. The location of the slot is called the address of the object. The address of an object is obtained using a function called a hash function. Each object has an associated key. The hash function takes the key as a parameter and returns the address of the object.
The primary operation it supports efficiently is a lookup: given a key (e.g. a person's name), find the corresponding value (e.g. that person's telephone number). It works by transforming the key using a hash function into a hash, a number that the hash table uses to locate the desired value.
Contents |
Hash Table Behavior
A good hash function should distribute the objects throughout the table with equal probability. A good hash function should minimize collisions. In addition, a good hash function should be easy to calculate.
For example, a simple hash function for a table of size M is:
FUNCTION hash( key )
RETURN (key % M);
ENDFUNCTION
However, this function works well only if the keys have an equal distribution.
Hash tables are often used to implement associative arrays, sets and caches. Like arrays, hash tables provide constant-time O(1) lookup on average, regardless of the number of items in the table. However, the rare worst-case lookup time can be as bad as O(n). Compared to other associative array data structures, hash tables are most useful when large numbers of records of data are to be stored.
Hash tables may be used as in-memory data structures. Hash tables may also be adopted for use with persistent data structures; database indexes commonly use disk-based data structures based on hash tables.
Other examples of hash functions: ELF (Executable and Linking Format [Unix System V]), and Soundex
Collision Resolution
If two keys hash to the same index, the corresponding records cannot be stored in the same location. So, if it's already occupied, we must find another location to store the new record, and do it so that we can find it when we look it up later on.
To give an idea of the importance of a good collision resolution strategy, consider the following result, derived using the birthday paradox. Even if we assume that our hash function outputs random indices uniformly distributed over the array, and even for an array with 1 million entries, there is a 95% chance of at least one collision occurring before it contains 2500 records.
There are two basic techniques of collision resolution: Open Hashing (also called Separate Chaining) and Closed Hashing (also called Open Addressing).
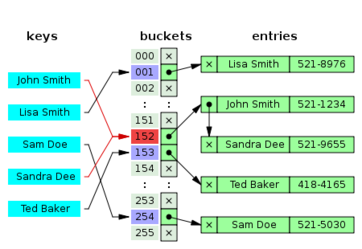
Open Hashing (Chaining)
Open Hashing or Chaining means that collisions are stored outside the table.
In the simplest chained hash table technique, each slot in the array references a linked list of inserted records that collide to the same slot. Insertion requires finding the correct slot, and appending to either end of the list in that slot; deletion requires searching the list and removal.
Chained hash tables have advantages over open addressed hash tables in that the removal operation is simple and resizing the table can be postponed for a much longer time because performance degrades more gracefully even when every slot is used. Indeed, many chaining hash tables may not require resizing at all since performance degradation is linear as the table fills. For example, a chaining hash table containing twice its recommended capacity of data would only be about twice as slow on average as the same table at its recommended capacity.
Chained hash tables inherit the disadvantages of linked lists. When storing small records, the overhead of the linked list can be significant. An additional disadvantage is that traversing a linked list has poor cache performance.
Alternative data structures can be used for chains instead of linked lists. By using a self-balancing tree, for example, the theoretical worst-case time of a hash table can be brought down to O(log n) rather than O(n). However, since each list is intended to be short, this approach is usually inefficient unless the hash table is designed to run at full capacity or there are unusually high collision rates, as might occur in input designed to cause collisions. Dynamic arrays can also be used to decrease space overhead and improve cache performance when records are small.
Some chaining implementations use an optimization where the first record of each chain is stored in the table. Although this can increase performance, it is generally not recommended: chaining tables with reasonable load factors contain a large proportion of empty slots, and the larger slot size causes them to waste large amounts of space.
Another version of open hashing is called Bucket Hashing. In bucket hashing, the slots of the table are organized into groups called buckets. The hash function returns a bucket number, and the item is inserted into an open slot in the bucket. If the bucket is full, there is an overflow area.
Closed Hashing (Open Addressing)
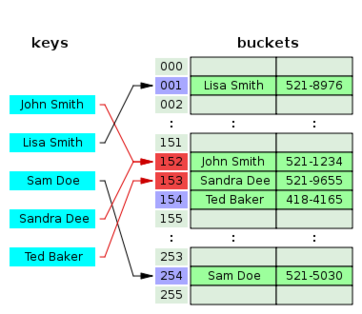
Open addressing hash tables can store the records directly within the array. A hash collision is resolved by probing, or searching through alternate locations in the array (the probe sequence) until either the target record is found, or an unused array slot is found, which indicates that there is no such key in the table. Well known probe sequences include:
- linear probing
- in which the interval between probes is fixed--often at 1,
- quadratic probing
- in which the interval between probes increases linearly (hence, the indices are described by a quadratic function), and
- double hashing
- in which the interval between probes is fixed for each record but is computed by another hash function.
In closed hashing, since the collisions are stored in the table itself, this can create a condition known as a secondary collision.
In probing, the hash function becomes:
h( k ) + p( i ), where i is an iteration value and p( 0 ) = 0.
The simplest of these is linear probing, where p( i ) = i. This, however, can result in a problem called clustering, which can increase the probability of secondary collisions.
Suppose the table has ten slots and the hash function gives an equal probability to any slot in the table. Thus the probability is 0.1 that a key hashes to any one slot. Now suppose that slots 0 through 3 are filled. Then the probability that the next value will end up in slot 4 is 0.5, because anything that hashes to slots 0, 1, 2, 3, or 4 will end up in slot 4.
In Quadratic Probing, the probe function is p( i ) = i^2. With quadratic probing, if the size of the table is a prime and the table is less than one-half full, an new element can always be inserted. However, if the table is more than half full, the insertion might fail.
A problem with probing is that the same sequence is used for all keys. So, as collisions occur, secondary collisions increase. An alternative to this is double hashing. Double hashing is defined by the function: h1( k ) + i * h2( k ). Note that it is important that h2( k ) not produce a 0. A good choice for a double hashing function is the let the table size be a prime number M and to let R be another prime that is less than M, then h2( k ) = R – ( k % R ).
The main tradeoffs between these methods are that linear probing has the best cache performance but is most sensitive to clustering, while double hashing has poor cache performance but exhibits virtually no clustering; quadratic hashing falls in-between in both areas. Double hashing can also require more computation than other forms of probing. Some open addressing methods, such as last-come-first-served hashing and cuckoo hashing move existing keys around in the array to make room for the new key. This gives better maximum search times than the methods based on probing.
Load Factor
A critical influence on performance of an open addressing hash table is the load factor; that is, the proportion of the slots in the array that are used. As the load factor increases towards 100%, the number of probes that may be required to find or insert a given key rises dramatically. Once the table becomes full, probing algorithms may even fail to terminate. Even with good hash functions, load factors are normally limited to 80%. A poor hash function can exhibit poor performance even at very low load factors by generating significant clustering. What causes hash functions to cluster is not well understood, and it is easy to unintentionally write a hash function which causes severe clustering.
The load factor α is defined to be N/M, where N is the number of records in the table and M is the size of the table. For open hashing, we generally want the load factor to be close to 1. For closed hashing, we generally want to load factor to be less that 0.5.
Deletions
When deleting records from a hash table, there are two important considerations.
- Deleting a record must not hinder later searches. That is, it must not cut off a chain used
for probing.
- A slot freed because of a deletion must remain usable.
One solution to these problems is to use a tombstone. A tombstone is a special marker that states that a slot is free; however, it used to be part of a chain. If a search encounters a tombstone, it should continue going. When inserting, however, to avoid duplicate values in the table, a search must still traverse the entire chain before reusing the tombstoned slot.
Tombstones do lengthen the size of chains. One possibility is that after a deletion, continue to follow a chain, swapping the tombstone with the value along the chain. In this manner, tombstones are always moved to the end of chains and are eventually reused.
ReHashing
When a table gets too full or when chains get too long due to tombstones, create another table at least twice the size of the original table and process each record, using a new hash function, and insert the records into the new table.
CS2: Data Structures
Theory of Computation - ADT Preliminaries
Linear ADTs - Tree ADTs - Graph ADTs - Unordered Collection ADTs