B-Trees

From

Begin

↑ Multi-Way_Trees

B+Trees →

A B-tree is a tree data structure that keeps data sorted and allows searches, insertions, and deletions in logarithmic amortized time. Unlike self-balancing binary search trees, it is optimized for systems that read and write large blocks of data. It is most commonly used in databases and filesystems.

In B-trees, internal (non-leaf) nodes can have a variable number of child nodes within some pre-defined range. When data are inserted or removed from a node, its number of child nodes changes. In order to maintain the pre-defined range, internal nodes may be joined or split. Because a range of child nodes is permitted, B-trees do not need re-balancing as frequently as other self-balancing search trees, but may waste some space, since nodes are not entirely full. The lower and upper bounds on the number of child nodes are typically fixed for a particular implementation. For example, in a 2-3 B-tree (often simply referred to as a 2-3 tree), each internal node may have only 2 or 3 child nodes.

A B-tree is kept balanced by requiring that all leaf nodes are at the same depth. This depth will increase slowly as elements are added to the tree, but an increase in the overall depth is infrequent, and results in all leaf nodes being one more node further away from the root.

B-trees have substantial advantages over alternative implementations when node access times far exceed access times within nodes. This usually occurs when most nodes are in secondary storage such as hard drives. By maximizing the number of child nodes within each internal node, the height of the tree decreases, balancing occurs less often, and efficiency increases. Usually this value is set such that each node takes up a full Block size disk block or an analogous size in secondary storage. While 2-3 B-trees might be useful in main memory, and are certainly easier to explain, if the node sizes are tuned to the size of a disk block, the result might be a 257-513 B-tree (where the sizes are related to larger powers of 2).

A B-tree of order m (the maximum number of children for each node) is a tree which satisfies the following properties:

1. Every node has at most m children.
2. Every node (except root and leaves) has at least Template:Frac children.
3. The root has at least two children if it is not a leaf node.
4. All leaves appear in the same level, and carry information.
5. A non-leaf node with k children contains k–1 keys

Rudolf Bayer and Ed McCreight invented the B-tree while working at Boeing^[1], but did not explain what, if anything, the B stands for. Douglas Comer suggests a number of possibilities:

"Balanced," "Broad," or "Bushy" might apply [since all leaves are at the same level]. Others suggest that the "B" stands for Boeing [since the authors worked at Boeing Scientific Research Labs in 1972]. Because of his contributions, however, it seems appropriate to think of B-trees as "Bayer"-trees.^[2]

Contents 1 Node structures 2 Best case and worst case heights 3 Algorithms 3.1 Search 3.2 Insertion 3.3 Deletion 3.3.1 Deletion from a leaf node 3.3.2 Deletion from an internal node 3.3.3 Rebalancing after deletion 3.4 Initial construction 4 Notes

Node structures

Each internal node's elements act as separation values which divide its subtrees. For example, if an internal node has three child nodes (or subtrees) then it must have two separation values or elements a₁ and a₂. All values in the leftmost subtree will be less than a₁ , all values in the middle subtree will be between a₁ and a₂, and all values in the rightmost subtree will be greater than a₂.

Internal nodes in a B-tree — nodes which are not leaf nodes — are usually represented as an ordered set of elements and child pointers. Every internal node contains a maximum of U children and — other than the root — a minimum of L children. For all internal nodes other than the root, the number of elements is one less than the number of child pointers; the number of elements is between L-1 and U-1. The number U must be either 2L or 2L-1; thus each internal node is at least half full. This relationship between U and L implies that two half-full nodes can be joined to make a legal node, and one full node can be split into two legal nodes (if there is room to push one element up into the parent). These properties make it possible to delete and insert new values into a B-tree and adjust the tree to preserve the B-tree properties.

Leaf nodes have the same restriction on the number of elements, but have no children, and no child pointers.

The root node still has the upper limit on the number of children, but has no lower limit. For example, when there are fewer than L-1 elements in the entire tree, the root will be the only node in the tree, and it will have no children at all.

A B-tree of depth n+1 can hold about U times as many items as a B-tree of depth n, but the cost of search, insert, and delete operations grows with the depth of the tree. As with any balanced tree, the cost grows much more slowly than the number of elements.

Some balanced trees store values only at the leaf nodes, and so have different kinds of nodes for leaf nodes and internal nodes. B-trees keep values in every node in the tree, and may use the same structure for all nodes. However, since leaf nodes never have children, a specialized structure for leaf nodes in B-trees will improve performance.

Best case and worst case heights

The best case height of a B-Tree is:

log_Mn

The worst case height of a B-Tree is:

Where M is the maximum number of children a node can have.

Algorithms

Search

Search is performed in the typical manner, analogous to that in a binary search tree. Starting at the root, the tree is traversed top to bottom, choosing the child pointer whose separation values are on either side of the value that is being searched.

Binary search is typically (but not necessarily) used within nodes to find the separation values and child tree of interest.

Insertion

All insertions happen at the leaf nodes.

1. By searching the tree, find the leaf node where the new element should be added.
2. If the leaf node contains fewer than the maximum legal number of elements, there is room for one more. Insert the new element in the node, keeping the node's elements ordered.
3. Otherwise the leaf node is split into two nodes.
   1. A single median is chosen from among the leaf's elements and the new element.
   2. Values less than the median are put in the new left node and values greater than the median are put in the new right node, with the median acting as a separation value.
   3. That separation value is added to the node's parent, which may cause it to be split, and so on.

If the splitting goes all the way up to the root, it creates a new root with a single separator value and two children, which is why the lower bound on the size of internal nodes does not apply to the root. The maximum number of elements per node is U-1. When a node is split, one element moves to the parent, but one element is added. So, it must be possible to divide the maximum number U-1 of elements into two legal nodes. If this number is odd, then U=2L and one of the new nodes contains (U-2)/2 = L-1 elements, and hence is a legal node, and the other contains one more element, and hence it is legal too. If U-1 is even, then U=2L-1, so there are 2L-2 elements in the node. Half of this number is L-1, which is the minimum number of elements allowed per node.

An improved algorithm supports a single pass down the tree from the root to the node where the insertion will take place, splitting any full nodes encountered on the way. This prevents the need to recall the parent nodes into memory, which may be expensive if the nodes are on secondary storage. However, to use this improved algorithm, we must be able to send one element to the parent and split the remaining U-2 elements into two legal nodes, without adding a new element. This requires U = 2L rather than U = 2L-1, which accounts for why some textbooks impose this requirement in defining B-trees.

Deletion

There are two popular strategies for deletion from a B-Tree.

• locate and delete the item, then restructure the tree to regain its invariants

or

• do a single pass down the tree, but before entering (visiting) a node, restructure the tree so that once the key to be deleted is encountered, it can be deleted without triggering the need for any further restructuring

The algorithm below uses the former strategy.

There are two special cases to consider when deleting an element:

1. the element in an internal node may be a separator for its child nodes
2. deleting an element may put it under the minimum number of elements and children.

Each of these cases will be dealt with in order.

Deletion from a leaf node

• Search for the value to delete.
• If the value is in a leaf node, it can simply be deleted from the node, perhaps leaving the node with too few elements; so some additional changes to the tree will be required.

Deletion from an internal node

Each element in an internal node acts as a separation value for two subtrees, and when such an element is deleted, two cases arise. In the first case, both of the two child nodes to the left and right of the deleted element have the minimum number of elements, namely L-1. They can then be joined into a single node with 2L-2 elements, a number which does not exceed U-1 and so is a legal node. Unless it is known that this particular B-tree does not contain duplicate data, we must then also (recursively) delete the element in question from the new node.

In the second case, one of the two child nodes contains more than the minimum number of elements. Then a new separator for those subtrees must be found. Note that the largest element in the left subtree is the largest element which is still less than the separator. Likewise, the smallest element in the right subtree is the smallest element which is still greater than the separator. Both of those elements are in leaf nodes, and either can be the new separator for the two subtrees.

• If the value is in an internal node, choose a new separator (either the largest element in the left subtree or the smallest element in the right subtree), remove it from the leaf node it is in, and replace the element to be deleted with the new separator.
• This has deleted an element from a leaf node, and so is now equivalent to the previous case.

Rebalancing after deletion

If deleting an element from a leaf node has brought it under the minimum size, some elements must be redistributed to bring all nodes up to the minimum. In some cases the rearrangement will move the deficiency to the parent, and the redistribution must be applied iteratively up the tree, perhaps even to the root. Since the minimum element count doesn't apply to the root, making the root be the only deficient node is not a problem. The algorithm to rebalance the tree is as follows:Template:Fact

• If the right sibling has more than the minimum number of elements.
  • Add the separator to the end of the deficient node.
  • Replace the separator in the parent with the first element of the right sibling.
  • Make the first child of the right sibling into the last child of the deficient node
• Otherwise, if the left sibling has more than the minimum number of elements.
  • Add the separator to the start of the deficient node.
  • Replace the separator in the parent with the last element of the left sibling.
  • Make the last child of the left sibling into the first child of the deficient node
• If both immediate siblings have only the minimum number of elements
  • Create a new node with all the elements from the deficient node, all the elements from one of its siblings, and the separator in the parent between the two combined sibling nodes.
  • Remove the separator from the parent, and replace the two children it separated with the combined node.
  • If that brings the number of elements in the parent under the minimum, repeat these steps with that deficient node, unless it is the root, since the root may be deficient.

The only other case to account for is when the root has no elements and one child. In this case it is sufficient to replace it with its only child.

Initial construction

In applications, it's frequently useful to build a B-tree to represent a large existing collection of data and then update it incrementally using standard B-tree operations. In this case, the most efficient way to construct the initial B-tree is not to insert every element in the initial collection successively, but instead to construct the initial set of leaf nodes directly from the input, then build the internal nodes from these. This approach to B-tree construction is called bulkloading. Initially, every leaf but the last one has one extra element, which will be used to build the internal nodes.Template:Fact

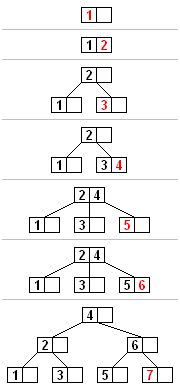
For example, if the leaf nodes have maximum size 4 and the initial collection is the integers 1 through 24, we would initially construct 5 leaf nodes containing 5 values each (except the last, which contains 4):

1 2 3 4 5

6 7 8 9 10

11 12 13 14 15

16 17 18 19 20

21 22 23 24

We build the next level up from the leaves by taking the last element from each leaf node except the last one. Again, each node except the last will contain one extra value. In the example, suppose the internal nodes contain at most 2 values (3 child pointers). Then the next level up of internal nodes would be:

5 10 15

20

1 2 3 4

6 7 8 9

11 12 13 14

16 17 18 19

21 22 23 24

This process is continued until we reach a level with only one node and it is not overfilled. In the example only the root level remains:

15
5 10	20

1 2 3 4

6 7 8 9

11 12 13 14

16 17 18 19

21 22 23 24

Notes

Template:Original research Each node will always have between L and U children, inclusively, with one exception: the root node may have anywhere from 2 to U children inclusively. In other words, the root is exempt from the lower bound restriction. This allows the tree to hold small numbers of elements. The root having one child makes no sense, since the subtree attached to that child could simply be attached to the root. Giving the root no children is also unnecessary, since a tree with no elements is typically represented as having no root node.

---

---