Hash Tables

From

Revision as of 18:37, 19 April 2009 by Admin (Talk | contribs)

(diff) ← Older revision | Current revision (diff) | Newer revision → (diff)

← Maps and Dictionaries

↑ Contents: CS2

End

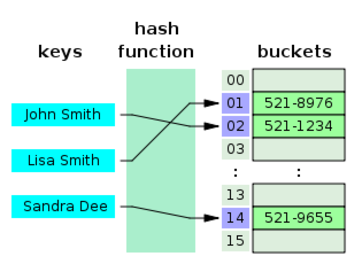
Hashing is called a Key to Address system. Objects (records) are stored in a table, and each object stored occupies a slot in the table. The location of the slot is called the address of the object. The address of an object is obtained using a function called a hash function. Each object has an associated key. The hash function takes the key as a parameter and returns the address of the object.

The primary operations that Hashing supports efficiently are a insertion and lookup: given a key (e.g. a person's name), find the corresponding location of that value (e.g. that person's telephone number). It works by transforming the key using a hash function into a hash, a number that the hash table uses to locate the desired value.

Hash Table Behavior

A small phone book as a hash table.

The goal of a hash table is to get Theta(1) lookup time, that is, constant lookup time. Rather than having to proceed through a Theta(n) sequence of comparisons as in linear search, or a Theta(lg n) sequence of comparisons as in binary search, a hash table will usually complete a lookup after just one comparison! Sometimes, however, two comparisons (or even more) are needed. A hash table thus delivers (almost) the ideal lookup time. The trade-off is that to get this great lookup time memory space is wasted. This may well be a good trade-off, however, as memory is cheap.

The idea is that we store records of data in the hash table, which is either an array (when main memory is used), or a file (if disk space is used). Each record has a key field and an associated data field. The record is stored in a location that is based on its key. The function that produces this location for each given key is called a hash function.

A good hash function should distribute the objects throughout the table with equal probability. A good hash function should minimize collisions. In addition, a good hash function should be easy to calculate.

For example, a simple hash function for a table of size M is:

FUNCTION hash( key )
    RETURN (key % M);
ENDFUNCTION

However, this function works well only if the keys have an equal distribution.

Hash tables are often used to implement associative arrays, sets and caches. Like arrays, hash tables provide constant-time O(1) lookup on average, regardless of the number of items in the table. However, the rare worst-case lookup time can be as bad as O(n). Compared to other associative array data structures, hash tables are most useful when large numbers of records of data are to be stored.

Hash tables may be used as in-memory data structures. Hash tables may also be adopted for use with persistent data structures; database indexes commonly use disk-based data structures based on hash tables.

Other examples of hash functions: ELF (Executable and Linking Format [Unix System V]), and Soundex

Hash Functions: hash(key)

Let's suppose that each key field contains an integer and the data field a string (array of characters type of string). One common basic hash function is:

hash(key) = key % prime

Recall that % is the mod operator that gives the remainder after integer division. The constant prime holds some prime number that is the length of the table. (For technical reasons, a prime number works better.) Perhaps we are storing our hash table in an array and use prime = 101. This means that our table can hold up to 101 records, at indices 0 through 100. If we want to insert 225 into the table we compute hash(225) as 225 % 101 = 23 and store the record containing key value 225 at index 23 in the array. Of course, if this location already contains a record, then we have a problem (called a collision). More on collisions in the next section.

If we go to look up the record with key 225, we again calculate hash(225) and get 23. We go to index 23, check that the record at that position has key value 225, and copy that record. There it is: one comparison and we completed our lookup. The situation is even more dramatic when using a file, since disk access is so much slower and every new record that has to be read adds appreciably to the lookup time. Here the hash function values are record numbers not array indices, but it works very much the same. To look up 225, we find hash(225) = 23, read record 23 from the file, check that this record does indeed have key value 225 and we are done! Only one record had to be read!

A good hash function should be quick to compute, produce all possible indices from 0 to prime - 1, and should minimize collisions. For integer keys, hash(key) = key % prime is typically used. For string keys, some method of converting the string to an integer is usually used, followed by taking result % prime to cut the integer value down to size. One also needs to worry about integer overflow. The hash value should ideally depend on every bit of the key. It is not good to ignore part of the key as that may lead to several keys that hash to the same location.

Here is one method for strings. Let's suppose that the strings only contain the letters of the alphabet, in upper case. In other words, we have the letters A through Z. We can translate the individual letters to the integers 0 through 25. Then we treat the string as a base 26 number. For example, CPU would be the base 26 number with digits 2, 15, 20. The decimal value of this number is 2(26^2) + 15(26) + 20. All computations are done % prime, both to avoid overflow, and because the final hash value must fit the range 0 to prime - 1. For example, if prime = 101, we would get 26^2 % 101 = 676 % 101 = 70. Then 2(26^2) % 101 = 39. The 15(26) % 101 = 390 % 101 = 87. Thus we get (39 + 87) % 101 = 126 % 101 = 25. The final hash value is thus (25 + 20) % 101 = 45. If your strings include more of the ASCII character set than this, you might want to use the ASCII value of each letter instead of mapping A to 0, B to 1, etc.

A folding method is sometimes used to hash integers. Here the key is chopped into two or more parts and the parts recombined in some easy manner. For example, suppose the keys are 9 digit longs, such as 542981703. Chop this into 3 equal-length pieces and add them together: 542 + 981 + 703, taking the sum % prime to cut the answer down to size.

Collision Resolution

If two keys hash to the same index, the corresponding records cannot be stored in the same location. So, if it's already occupied, we must find another location to store the new record, and do it so that we can find it when we look it up later on.

To give an idea of the importance of a good collision resolution strategy, consider the following result, derived using the birthday paradox. Even if we assume that our hash function outputs random indices uniformly distributed over the array, and even for an array with 1 million entries, there is a 95% chance of at least one collision occurring before it contains 2500 records.

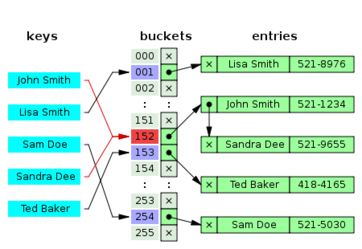
There are two basic techniques of collision resolution: Open Hashing (also called Separate Chaining) and Closed Hashing (also called Open Addressing).

Open Hashing (or Separate Chaining)

Open hashing or separate chaining means that collisions are stored outside the table.

Hash collision resolved by chaining.

In the simplest chained hash table technique, each slot in the array references a linked list of inserted records that collide to the same slot. Insertion requires finding the correct slot, and appending to either end of the list in that slot; deletion requires searching the list and removal.

Chained hash tables have advantages over open addressed hash tables in that the removal operation is simple and resizing the table can be postponed for a much longer time because performance degrades more gracefully even when every slot is used. Indeed, many chaining hash tables may not require resizing at all since performance degradation is linear as the table fills. For example, a chaining hash table containing twice its recommended capacity of data would only be about twice as slow on average as the same table at its recommended capacity.

Chained hash tables inherit the disadvantages of linked lists. When storing small records, the overhead of the linked list can be significant. An additional disadvantage is that traversing a linked list has poor cache performance.

Alternative data structures can be used for chains instead of linked lists. By using a self-balancing tree, for example, the theoretical worst-case time of a hash table can be brought down to O(log n) rather than O(n). However, since each list is intended to be short, this approach is usually inefficient unless the hash table is designed to run at full capacity or there are unusually high collision rates, as might occur in input designed to cause collisions. Dynamic arrays can also be used to decrease space overhead and improve cache performance when records are small.

Some chaining implementations use an optimization where the first record of each chain is stored in the table. Although this can increase performance, it is generally not recommended: chaining tables with reasonable load factors contain a large proportion of empty slots, and the larger slot size causes them to waste large amounts of space.

Another version of open hashing is called Bucket Hashing. In bucket hashing, the slots of the table are organized into groups called buckets. The hash function returns a bucket number, and the item is inserted into an open slot in the bucket. If the bucket is full, there is an overflow area.

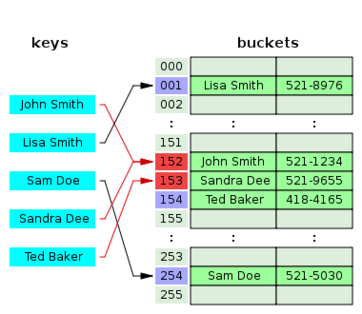
Closed Hashing (Open Addressing)

Hash collision resolved by linear probing (interval=1).

Open addressing hash tables can store the records directly within the array. A hash collision is resolved by probing, or searching through alternate locations in the array (the probe sequence) until either the target record is found, or an unused array slot is found, which indicates that there is no such key in the table. Well known probe sequences include:

linear probing: in which the interval between probes is fixed--often at 1,
quadratic probing: in which the interval between probes increases linearly (hence, the indices are described by a quadratic function), and
double hashing: in which the interval between probes is fixed for each record but is computed by another hash function.

In closed hashing, since the collisions are stored in the table itself, this can create a condition known as a secondary collision. Secondary collisions can result from the previous fix to a primary collision; some key/value was placed into the table in a location other than it's actual hash location. The secondary collision occurs when trying to add a key/value into it's hash slot and the slot is already occupied occupied by a key/value that does not directly hash to that location.

In probing, the hash function becomes:

h( k ) + p( i ), where i is an iteration value and p( 0 ) = 0.

The simplest of these is linear probing, where p( i ) = i. This, however, can result in a problem called clustering, which can increase the probability of secondary collisions.

Suppose the table has ten slots and the hash function gives an equal probability to any slot in the table. Thus the probability is 0.1 that a key hashes to any one slot. Now suppose that slots 0 through 3 are filled. Then the probability that the next value will end up in slot 4 is 0.5, because anything that hashes to slots 0, 1, 2, 3, or 4 will end up in slot 4.

In Quadratic Probing, the probe function is p( i ) = i^2. With quadratic probing, if the size of the table is a prime and the table is less than one-half full, an new element can always be inserted. However, if the table is more than half full, the insertion might fail.

A problem with probing is that the same sequence is used for all keys. So, as collisions occur, secondary collisions increase. An alternative to this is double hashing. Double hashing is defined by the function: h1( k ) + i * h2( k ). Note that it is important that h2( k ) not produce a 0. A good choice for a double hashing function is the let the table size be a prime number M and to let R be another prime that is less than M, then h2( k ) = R – ( k % R ).

The main tradeoffs between these methods are that linear probing has the best cache performance but is most sensitive to clustering, while double hashing has poor cache performance but exhibits virtually no clustering; quadratic hashing falls in-between in both areas. Double hashing can also require more computation than other forms of probing. Some open addressing methods, such as last-come-first-served hashing and cuckoo hashing move existing keys around in the array to make room for the new key. This gives better maximum search times than the methods based on probing.

Load Factor

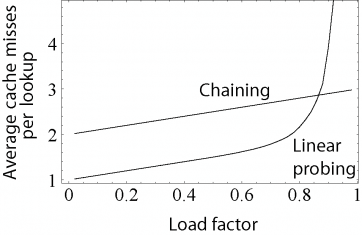
A critical influence on performance of an open addressing hash table is the load factor; that is, the proportion of the slots in the array that are used. As the load factor increases towards 100%, the number of probes that may be required to find or insert a given key rises dramatically. Once the table becomes full, probing algorithms may even fail to terminate. Even with good hash functions, load factors are normally limited to 80%. A poor hash function can exhibit poor performance even at very low load factors by generating significant clustering. What causes hash functions to cluster is not well understood, and it is easy to unintentionally write a hash function which causes severe clustering.

The load factor α is defined to be N/M, where N is the number of records in the table and M is the size of the table. For open hashing, we generally want the load factor to be close to 1. For closed hashing, we generally want to load factor to be less that 0.5.

Open addressing versus chaining

Chained hash tables have the following benefits over open addressing:

They are simple to implement effectively and only require basic data structures.
From the point of view of writing suitable hash functions, chained hash tables are insensitive to clustering, only requiring minimization of collisions. Open addressing depends upon better hash functions to avoid clustering. This is particularly important if novice programmers can add their own hash functions, but even experienced programmers can be caught out by unexpected clustering effects.
They degrade in performance more gracefully. Although chains grow longer as the table fills, a chained hash table cannot "fill up" and does not exhibit the sudden increases in lookup times that occur in a near-full table with open addressing. (see right)
If the hash table stores large records, about 5 or more words per record, chaining uses less memory than open addressing.
If the hash table is sparse (that is, it has a big array with many free array slots), chaining uses less memory than open addressing even for small records of 2 to 4 words per record due to its external storage.

This graph compares the average number of cache misses required to lookup elements in tables with chaining and linear probing. As the table passes the 80%-full mark, linear probing's performance drastically degrades.

For small record sizes (a few words or less) the benefits of in-place open addressing compared to chaining are:

They can be more space-efficient than chaining since they don't need to store any pointers or allocate any additional space outside the hash table. Simple linked lists require a word of overhead per element.
Insertions avoid the time overhead of memory allocation, and can even be implemented in the absence of a memory allocator.
Because it uses internal storage, open addressing avoids the extra indirection required for chaining's external storage. It also has better locality of reference, particularly with linear probing. With small record sizes, these factors can yield better performance than chaining, particularly for lookups.
They can be easier to serialize, because they don't use pointers.

On the other hand, normal open addressing is a poor choice for large elements, since these elements fill entire cache lines (negating the cache advantage), and a large amount of space is wasted on large empty table slots. If the open addressing table only stores references to elements (external storage), it uses space comparable to chaining even for large records but loses its speed advantage.

Generally speaking, open addressing is better used for hash tables with small records that can be stored within the table (internal storage) and fit in a cache line. They are particularly suitable for elements of one word or less. In cases where the tables are expected to have high load factors, the records are large, or the data is variable-sized, chained hash tables often perform as well or better.

Ultimately, used sensibly any kind of hash table algorithm is usually fast enough; and the percentage of a calculation spent in hash table code is low. Memory usage is rarely considered excessive. Therefore, in most cases the differences between these algorithms is marginal, and other considerations typically come into play.

Deletions

When deleting records from a hash table, there are two important considerations.

Deleting a record must not hinder later searches. That is, it must not cut off a chain used for probing.
A slot freed because of a deletion must remain usable.

One solution to these problems is to use a tombstone. A tombstone is a special marker that states that a slot is free; however, it used to be part of a chain. If a search encounters a tombstone, it should continue going. When inserting, however, to avoid duplicate values in the table, a search must still traverse the entire chain before reusing the tombstoned slot.

Tombstones do lengthen the size of chains. One possibility is that after a deletion, continue to follow a chain, swapping the tombstone with the value along the chain. In this manner, tombstones are always moved to the end of chains and are eventually reused.

ReHashing

When a table gets too full or when chains get too long due to tombstones, create another table at least twice the size of the original table and process each record, using a new hash function, and insert the records into the new table.

Problems with hash tables

Ordered retrieval issue

Hash tables store data in pseudo-random locations, so accessing the data in a sorted manner is a very time consuming operation. Other data structures such as self-balancing binary search trees generally operate more slowly (since their lookup time is O(log n)) and are rather more complex to implement than hash tables but maintain a sorted data structure at all times.

Large constant time for Hash Function

Although hash table lookups use constant time on average, the time spent can be significant. Evaluating a good hash function can be a slow operation. In particular, if simple array indexing can be used instead, this is usually faster.

Poor locality of reference

Hash tables in general exhibit poor locality of reference—that is, the data to be accessed is distributed seemingly at random in memory. Because hash tables cause access patterns that jump around, this can trigger microprocessor cache misses that cause long delays. Compact data structures such as arrays, searched with linear search, may be faster if the table is relatively small and keys are cheap to compare, such as with simple integer keys. According to Moore's Law, cache sizes are growing exponentially and so what is considered "small" may be increasing. The optimal performance point varies from system to system; for example, a trial on the Parrot virtual machine shows that its hash tables outperform linear search in all but the most trivial cases (one to three entries).

Coding complexity

More significantly, hash tables are more difficult and error-prone to write and use. Hash tables require the design of an effective hash function for each key type, which in many situations is more difficult and time-consuming to design and debug than the mere comparison function required for a self-balancing binary search tree. In open-addressed hash tables it's even easier to create a poor hash function.

Prone to hacking

Additionally, in some applications, a black hat with knowledge of the hash function may be able to supply information to a hash which creates worst-case behavior by causing excessive collisions, resulting in very poor performance (i.e., a denial of service attack). In critical applications, either universal hashing can be used or a data structure with better worst-case guarantees may be preferable. For details, see Crosby and Wallach's Denial of Service via Algorithmic Complexity Attacks.