Tree ADTs
From
(→Glossary of terms for rooted trees) |
(→Terminology) |
||
| Line 12: | Line 12: | ||
==Terminology== | ==Terminology== | ||
| - | A node is a structure which may contain a value or a condition or represent a separate data structure or a tree of its own. Each node in a tree has zero or more '''child nodes''' two child for binary tree, which are below it in the tree (by convention, trees grow down, not up as they do in nature). A node that has a child is called the child's '''parent node''' (or ''ancestor node'', or | + | A node is a structure which may contain a value or a condition or represent a separate data structure or a tree of its own. Each node in a tree has zero or more '''child nodes''' two child for binary tree, which are below it in the tree (by convention, trees grow down, not up as they do in nature). A node that has a child is called the child's '''parent node''' (or ''ancestor node'', or superior). A node has at most one parent. |
<br/><br/> | <br/><br/> | ||
| - | The '''height''' of a node is the length of the longest downward path to a leaf from that node. The height of the root is the height of the tree. The '''depth''' of a node is the length of the path to its root (i.e., its ''root path''). Thus the depth of the root is 0. This is commonly needed in the manipulation of the various self balancing trees, | + | The '''height''' of a node is the length of the longest downward path to a leaf from that node. The height of the root is the height of the tree. The '''depth''' of a node is the length of the path to its root (i.e., its ''root path''). Thus the depth of the root is 0. This is commonly needed in the manipulation of the various self balancing trees, AVL Trees in particular. Conventionally, the value -1 corresponds to a subtree with no nodes, whereas zero corresponds to a subtree with one node. The '''height''' of the tree is 1 more than the depth of the deepest node. All nodes at depth d are said to be at '''level''' d. |
<br/><br/> | <br/><br/> | ||
| - | The topmost node in a tree is called the '''root node'''. Being the topmost node, the root node will not have parents. It is the node at which operations on the tree commonly begin (although some algorithms begin with the leaf nodes and work up ending at the root). All other nodes can be reached from it by following '''edges''' or '''links'''. (In the formal definition, each such path is also unique). In diagrams, it is typically drawn at the top. In some trees, such as | + | The topmost node in a tree is called the '''root node'''. Being the topmost node, the root node will not have parents. It is the node at which operations on the tree commonly begin (although some algorithms begin with the leaf nodes and work up ending at the root). All other nodes can be reached from it by following '''edges''' or '''links'''. (In the formal definition, each such path is also unique). In diagrams, it is typically drawn at the top. In some trees, such as heaps, the root node has special properties. Every node in a tree can be seen as the root node of the subtree rooted at that node. |
<br/><br/> | <br/><br/> | ||
Nodes at the bottommost level of the tree are called '''leaf nodes'''. Since they are at the bottommost level, they do not have any children. | Nodes at the bottommost level of the tree are called '''leaf nodes'''. Since they are at the bottommost level, they do not have any children. | ||
| Line 29: | Line 29: | ||
A '''subtree''' is a portion of a tree data structure that can be viewed as a complete tree in itself. Any node in a tree ''T'', together with all the nodes below it, comprise a subtree of ''T''. The subtree corresponding to the root node is the entire tree; the subtree corresponding to any other node is called is a '''proper subtree''' (in analogy to the term proper subset). | A '''subtree''' is a portion of a tree data structure that can be viewed as a complete tree in itself. Any node in a tree ''T'', together with all the nodes below it, comprise a subtree of ''T''. The subtree corresponding to the root node is the entire tree; the subtree corresponding to any other node is called is a '''proper subtree''' (in analogy to the term proper subset). | ||
<br/><br/> | <br/><br/> | ||
| + | ==Glossary of terms for rooted trees== | ||
| + | * A '''directed edge''' refers to the link from the [[Parent node|parent]] to the [[Child node|child]] (the arrows in the picture of the tree). | ||
| + | * The [[root node]] of a tree is the [[node (computer science)|node]] with no parents. There is at most one root node in a rooted tree. | ||
| + | * A [[leaf node]] has no children. | ||
| + | * The '''depth''' of a node n is the length of the path from the root to the node. The set of all nodes at a given depth is sometimes called a '''level''' of the tree. The root node is at depth zero. | ||
| + | * The '''height''' of a tree is the length of the path from the root to the deepest node in the tree. A (rooted) tree with only a node (the root) has a height of zero. | ||
| + | * '''Siblings''' are nodes that share the same parent node. | ||
| + | * If a path exists from node p to node q, where node p is closer to the root node than q, then p is an '''ancestor''' of q and q is a '''descendant''' of p. | ||
| + | * The '''size''' of a node is the number of descendants it has including itself. | ||
| + | *'''In-degree''' of a node is the number of edges arriving at that node. | ||
| + | * '''Out-degree''' of a node is the number of edges leaving that node. | ||
| + | *Root is the only node in the tree with In-degree = 0 | ||
== Paths == | == Paths == | ||
Revision as of 06:40, 12 May 2009
| Begin | ↑ Contents: CS2 | Binary Trees → |
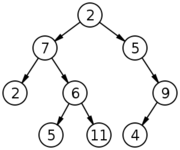
A tree is a finite set of elements called nodes. The set is either empty, or consists of a node called the root together with any number of successors which are also trees (subtrees in this case), which are disjoint from each other and from the root. The roots of the subtrees are called children of the root, and there is an edge from each node to its children, and a node is said to be the parent of its children. A node that has at least one child is called an internal node, and a node that has no children is called a leaf node.
More formally, in computer science, a tree is an acyclic connected graph where each node has a set of zero or more children nodes, and at most one parent node.
Contents |
Terminology
A node is a structure which may contain a value or a condition or represent a separate data structure or a tree of its own. Each node in a tree has zero or more child nodes two child for binary tree, which are below it in the tree (by convention, trees grow down, not up as they do in nature). A node that has a child is called the child's parent node (or ancestor node, or superior). A node has at most one parent.
The height of a node is the length of the longest downward path to a leaf from that node. The height of the root is the height of the tree. The depth of a node is the length of the path to its root (i.e., its root path). Thus the depth of the root is 0. This is commonly needed in the manipulation of the various self balancing trees, AVL Trees in particular. Conventionally, the value -1 corresponds to a subtree with no nodes, whereas zero corresponds to a subtree with one node. The height of the tree is 1 more than the depth of the deepest node. All nodes at depth d are said to be at level d.
The topmost node in a tree is called the root node. Being the topmost node, the root node will not have parents. It is the node at which operations on the tree commonly begin (although some algorithms begin with the leaf nodes and work up ending at the root). All other nodes can be reached from it by following edges or links. (In the formal definition, each such path is also unique). In diagrams, it is typically drawn at the top. In some trees, such as heaps, the root node has special properties. Every node in a tree can be seen as the root node of the subtree rooted at that node.
Nodes at the bottommost level of the tree are called leaf nodes. Since they are at the bottommost level, they do not have any children. They are also referred to as terminal nodes.
An internal node or inner node is any node of a tree that has child nodes and is thus not a leaf node.
A subtree is a portion of a tree data structure that can be viewed as a complete tree in itself. Any node in a tree T, together with all the nodes below it, comprise a subtree of T. The subtree corresponding to the root node is the entire tree; the subtree corresponding to any other node is called is a proper subtree (in analogy to the term proper subset).
Glossary of terms for rooted trees
- A directed edge refers to the link from the parent to the child (the arrows in the picture of the tree).
- The root node of a tree is the node with no parents. There is at most one root node in a rooted tree.
- A leaf node has no children.
- The depth of a node n is the length of the path from the root to the node. The set of all nodes at a given depth is sometimes called a level of the tree. The root node is at depth zero.
- The height of a tree is the length of the path from the root to the deepest node in the tree. A (rooted) tree with only a node (the root) has a height of zero.
- Siblings are nodes that share the same parent node.
- If a path exists from node p to node q, where node p is closer to the root node than q, then p is an ancestor of q and q is a descendant of p.
- The size of a node is the number of descendants it has including itself.
- In-degree of a node is the number of edges arriving at that node.
- Out-degree of a node is the number of edges leaving that node.
- Root is the only node in the tree with In-degree = 0
Paths
If n1, n2, …, nn is a sequence of nodes in the tree such that ni is the parent of ni+1, then this sequence is called a path. The length of the path is the number of edges, which is one less than the number of node: in this case the length of the path is n-1. If there is a path from a node M to a node N, then N is called a descendent of M and M is called an ancestor of N.
Trees
CS2: Data Structures
Theory of Computation - ADT Preliminaries
Linear ADTs - Tree ADTs - Graph ADTs - Unordered Collection ADTs