Binary Search Trees
From
m (→Removing an Element from a Binary Search Tree) |
|||
| (14 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | An important and frequently used specialization of a binary tree is a '''Binary Search Tree'''. | + | <noinclude> |
| - | binary search tree contains data that is ''comparable'', for example numbers or text, and has the | + | {{CS2:BookNav|base=/|up=Binary Trees|prev=|next=AVL Trees}} |
| + | </noinclude> | ||
| + | <br/> | ||
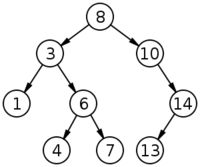
| + | [[Image:Binary search tree.svg|right|200px|thumb|A binary search tree of size 9 and depth 3, with root 8 and leaves 1, 4, 7 and 13]] | ||
| + | An important and frequently used specialization of a binary tree is a '''Binary Search Tree''' ('''BST''') which has the following properties: | ||
| + | * Each node (item in the tree) has a distinct value. | ||
| + | * Both the left and right subtrees must also be binary search trees. | ||
| + | * The left subtree of a node contains only values less than the node's value. | ||
| + | * The right subtree of a node contains only values greater than the node's value. | ||
| + | <br/> | ||
| + | The major advantage of binary search trees over other data structures is that the related sorting algorithms and search algorithms such as in-order traversal can be very efficient. | ||
| + | <br/><br/> | ||
| + | Binary search trees can choose to allow or disallow duplicate values, depending on the implementation. | ||
| + | <br/><br/> | ||
| + | Binary search trees are a fundamental data structure used to construct more abstract data structures such as sets, multisets, and associative arrays. | ||
| + | <br/><br/> | ||
| + | A binary search tree contains data that is ''comparable'', for example numbers or text, and has the | ||
following property: | following property: | ||
<br/><br/> | <br/><br/> | ||
| Line 6: | Line 22: | ||
Binary Search Tree Property: If '''N''' is a node in the tree, and '''N''' contains data '''D''', then all nodes in the left subtree of '''N''' contain data that is less than or equal to '''D''' and all nodes in the right subtree of '''N''' contain data that is greater than '''D'''. | Binary Search Tree Property: If '''N''' is a node in the tree, and '''N''' contains data '''D''', then all nodes in the left subtree of '''N''' contain data that is less than or equal to '''D''' and all nodes in the right subtree of '''N''' contain data that is greater than '''D'''. | ||
</blockquote> | </blockquote> | ||
| + | <br><br> | ||
| + | |||
== Searching for an Element in a Binary Search Tree == | == Searching for an Element in a Binary Search Tree == | ||
| + | Suppose I want to know if a value X is in the tree. I can search for X using the following algorithm. | ||
| + | <br/><br/> | ||
| + | <pre> | ||
| + | LET Found = false | ||
| + | LET P = the root of the tree | ||
| + | WHILE not Found and P is not NULL do | ||
| + | IF P.Data equals X | ||
| + | set Found to TRUE | ||
| + | ELSE IF P.Data < X | ||
| + | set P to P.right | ||
| + | ELSE | ||
| + | set P to P.left | ||
| + | ENDIF | ||
| + | ENDWHILE | ||
| + | </pre> | ||
| + | <br/> | ||
| + | Why is a search tree such a good organization for data? Suppose I have a list of names that are stored in a binary search tree and suppose there are 1,000,000 names in the tree. I am given a name, and I want to know if that name is in the list. What is the most number of checks I will have to make to determine if the name is in the list or not? At most, log2(1,000,000) = 20 checks will have to be made. | ||
| + | <br/><br/> | ||
== Inserting an Element into a Binary Search Tree == | == Inserting an Element into a Binary Search Tree == | ||
| + | |||
| + | Let P be a pointer to a tree node that is to be inserted into the tree. And, let Q be another pointer to a tree node that is initialized to the root of the tree.<br><br> | ||
| + | <pre>IF Q is NULL, THEN | ||
| + | The node that is pointed to by P becomes the root of the tree. | ||
| + | ELSE | ||
| + | Let Inserted be a Boolean value initialized to False | ||
| + | ENDIF | ||
| + | |||
| + | WHILE (not Inserted) | ||
| + | IF (P.Data <= Q.Data) | ||
| + | If (Q.Left is null) | ||
| + | Set Q.Left to P | ||
| + | Set Inserted to True | ||
| + | ELSE | ||
| + | Set Q to Q.Left | ||
| + | ENDIF | ||
| + | ELSE | ||
| + | IF( Q.Right is null) | ||
| + | Set Q.Right to P | ||
| + | Set Inserted to True | ||
| + | ELSE | ||
| + | Set Q to Q.Right | ||
| + | ENDIF | ||
| + | ENDIF | ||
| + | ENDWHILE | ||
| + | </pre> | ||
| + | <br/><br/> | ||
== Removing an Element from a Binary Search Tree == | == Removing an Element from a Binary Search Tree == | ||
| + | This operation is a little more complex. First we must find the node to be removed. Let P be | ||
| + | a node pointer that starts at the root and traverses the tree until it finds the node to be | ||
| + | removed. We need to consider three cases. | ||
| + | <br/><br/> | ||
| + | |||
| + | ''First case'': The node pointed to by P has no children. This means that P points to a leaf node | ||
| + | and is easy to delete. We just set P’s parent pointer to null and we are done. Of course there | ||
| + | is an implementation issue: If P points to the node to be deleted, how do we access the parent | ||
| + | of P? One solution to is problem is to use a second pointer Q. When P traverses the tree | ||
| + | looking for the node to be deleted, Q is set to P before moving P. In this way, Q always | ||
| + | points to the parent of the node that P points to. | ||
| + | <br/><br/> | ||
| + | |||
| + | ''Second case'': The node pointed to by P has one child. In this case, we just set P’s parent to | ||
| + | point to P’s child. | ||
| + | <br/><br/> | ||
| + | |||
| + | ''Third case'': P has two children. First find the node in the tree that is the in-order predecessor (previous smaller value in a sorted list) or the in-order successor (next larger value). | ||
| + | To get the in-order predecessor of P let T be a node pointer that is initialized to P’s left child. As long as T.Right is not null, let T = T.Right. Now swap the values in the nodes pointed to by P and T and delete the node pointed to by T (which will always be a no child or single child node). | ||
| + | <br/><br/> | ||
| + | |||
| + | One difficulty of a BST is that frequent insertions and deletions tend to make the tree out of | ||
| + | balance. The search time for an out-of-balance BST degenerates to that of a linked list. Two | ||
| + | approaches to this are AVL trees and Red-Black trees. | ||
| + | <br/><br/> | ||
| + | ---- | ||
| + | {{CS2/ChapNav}} | ||
| + | ---- | ||
| + | [[Category:CS2|{{SUBPAGENAME}}]] | ||
Current revision as of 14:32, 3 December 2014
| Begin | ↑ Binary Trees | AVL Trees → |
An important and frequently used specialization of a binary tree is a Binary Search Tree (BST) which has the following properties:
- Each node (item in the tree) has a distinct value.
- Both the left and right subtrees must also be binary search trees.
- The left subtree of a node contains only values less than the node's value.
- The right subtree of a node contains only values greater than the node's value.
The major advantage of binary search trees over other data structures is that the related sorting algorithms and search algorithms such as in-order traversal can be very efficient.
Binary search trees can choose to allow or disallow duplicate values, depending on the implementation.
Binary search trees are a fundamental data structure used to construct more abstract data structures such as sets, multisets, and associative arrays.
A binary search tree contains data that is comparable, for example numbers or text, and has the following property:
Binary Search Tree Property: If N is a node in the tree, and N contains data D, then all nodes in the left subtree of N contain data that is less than or equal to D and all nodes in the right subtree of N contain data that is greater than D.
Searching for an Element in a Binary Search Tree
Suppose I want to know if a value X is in the tree. I can search for X using the following algorithm.
LET Found = false
LET P = the root of the tree
WHILE not Found and P is not NULL do
IF P.Data equals X
set Found to TRUE
ELSE IF P.Data < X
set P to P.right
ELSE
set P to P.left
ENDIF
ENDWHILE
Why is a search tree such a good organization for data? Suppose I have a list of names that are stored in a binary search tree and suppose there are 1,000,000 names in the tree. I am given a name, and I want to know if that name is in the list. What is the most number of checks I will have to make to determine if the name is in the list or not? At most, log2(1,000,000) = 20 checks will have to be made.
Inserting an Element into a Binary Search Tree
Let P be a pointer to a tree node that is to be inserted into the tree. And, let Q be another pointer to a tree node that is initialized to the root of the tree.
IF Q is NULL, THEN
The node that is pointed to by P becomes the root of the tree.
ELSE
Let Inserted be a Boolean value initialized to False
ENDIF
WHILE (not Inserted)
IF (P.Data <= Q.Data)
If (Q.Left is null)
Set Q.Left to P
Set Inserted to True
ELSE
Set Q to Q.Left
ENDIF
ELSE
IF( Q.Right is null)
Set Q.Right to P
Set Inserted to True
ELSE
Set Q to Q.Right
ENDIF
ENDIF
ENDWHILE
Removing an Element from a Binary Search Tree
This operation is a little more complex. First we must find the node to be removed. Let P be a node pointer that starts at the root and traverses the tree until it finds the node to be removed. We need to consider three cases.
First case: The node pointed to by P has no children. This means that P points to a leaf node and is easy to delete. We just set P’s parent pointer to null and we are done. Of course there is an implementation issue: If P points to the node to be deleted, how do we access the parent of P? One solution to is problem is to use a second pointer Q. When P traverses the tree looking for the node to be deleted, Q is set to P before moving P. In this way, Q always points to the parent of the node that P points to.
Second case: The node pointed to by P has one child. In this case, we just set P’s parent to point to P’s child.
Third case: P has two children. First find the node in the tree that is the in-order predecessor (previous smaller value in a sorted list) or the in-order successor (next larger value). To get the in-order predecessor of P let T be a node pointer that is initialized to P’s left child. As long as T.Right is not null, let T = T.Right. Now swap the values in the nodes pointed to by P and T and delete the node pointed to by T (which will always be a no child or single child node).
One difficulty of a BST is that frequent insertions and deletions tend to make the tree out of balance. The search time for an out-of-balance BST degenerates to that of a linked list. Two approaches to this are AVL trees and Red-Black trees.
CS2: Data Structures
Theory of Computation - ADT Preliminaries
Linear ADTs - Tree ADTs - Graph ADTs - Unordered Collection ADTs