Common Graph Algorithms
From
(→Minimum Spanning Tree algorithms) |
(→Applications of Shortest Path Algrithms) |
||
| (3 intermediate revisions not shown) | |||
| Line 22: | Line 22: | ||
Formally, given a weighted graph (that is, a set ''V'' of vertices, a set ''E'' of edges, and a real-valued weight function ''f'' : ''E'' → '''R'''), and one element ''v'' of ''V'', find a path ''P'' from ''v'' to each ''v''' of ''V'' so that | Formally, given a weighted graph (that is, a set ''V'' of vertices, a set ''E'' of edges, and a real-valued weight function ''f'' : ''E'' → '''R'''), and one element ''v'' of ''V'', find a path ''P'' from ''v'' to each ''v''' of ''V'' so that | ||
| - | + | <br/><br/> | |
| - | + | <math>\sum_{p\in P} f(p)</math> | |
| - | + | <br/><br/> | |
is minimal among all paths connecting ''v'' to ''v''' . | is minimal among all paths connecting ''v'' to ''v''' . | ||
| Line 48: | Line 48: | ||
Other applications include "operations research, plant and facility layout, robotics, transportation, and Very-large-scale integration design".<ref>Danny Z. Chen. Developing Algorithms and Software for Geometric Path Planning Problems. ''ACM Computing Surveys'' 28A(4), December 1996.</ref> | Other applications include "operations research, plant and facility layout, robotics, transportation, and Very-large-scale integration design".<ref>Danny Z. Chen. Developing Algorithms and Software for Geometric Path Planning Problems. ''ACM Computing Surveys'' 28A(4), December 1996.</ref> | ||
| + | ---- | ||
| + | {{CS2/ChapNav}} | ||
| + | ---- | ||
| + | [[Category:CS2|{{SUBPAGENAME}}]] | ||
Revision as of 17:10, 9 April 2009
Contents |
Graph depth-first traversal
Same algorithm as with the tree ADT, but you have to check for nodes that have already been visited, usually by marking the node somehow.
Details to be written..
Graph breadth-first traversal
Same algorithm as with the tree ADT, but you have to check for nodes that have already been visited, usually by marking the node somehow.
Details to be written..
Minimum Spanning Tree algorithms
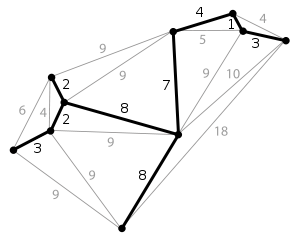
Given a connected graph, undirected graph, a spanning tree of that graph is a subgraph which is a tree and connects all the vertices together. A single graph can have many different spanning trees. We can also assign a weight to each edge, which is a number representing how unfavorable it is, and use this to assign a weight to a spanning tree by computing the sum of the weights of the edges in that spanning tree. A minimum spanning tree (MST) or minimum weight spanning tree is then a spanning tree with weight less than or equal to the weight of every other spanning tree. More generally, any undirected graph (not necessarily connected) has a minimum spanning forest, which is a union of minimum spanning trees for its connected components.
One example would be a cable TV company laying cable to a new neighborhood. If it is constrained to bury the cable only along certain paths, then there would be a graph representing which points are connected by those paths. Some of those paths might be more expensive, because they are longer, or require the cable to be buried deeper; these paths would be represented by edges with larger weights. A spanning tree for that graph would be a subset of those paths that has no cycles but still connects to every house. There might be several spanning trees possible. A minimum spanning tree would be one with the lowest total cost.
Shortest Path algorithms
In graph theory, the shortest path problem is the problem of finding a path between two vertices (or nodes) such that the sum of the weights of its constituent edges is minimized. An example is finding the quickest way to get from one location to another on a road map; in this case, the vertices represent locations and the edges represent segments of road and are weighted by the time needed to travel that segment.
Formally, given a weighted graph (that is, a set V of vertices, a set E of edges, and a real-valued weight function f : E → 'R), and one element v of V, find a path P from v to each v of V so that
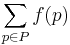
is minimal among all paths connecting v to v' .
The problem is also sometimes called the single-pair shortest path problem, to distinguish it from the following generalizations:
- The single-source shortest path problem, in which we have to find shortest paths from a source vertex v to all other vertices in the graph.
- The single-destination shortest path problem, in which we have to find shortest paths from all vertices in the graph to a single destination vertex v. This can be reduced to the single-source shortest path problem by reversing the edges in the graph.
- The all-pairs shortest path problem', in which we have to find shortest paths between every pair of vertices v, v in the graph.
These generalizations have significantly more efficient algorithms than the simplistic approach of running a single-pair shortest path algorithm on all relevant pairs of vertices.
Applications of Shortest Path Algrithms
Shortest path algorithms are applied to automatically find directions between physical locations, such as driving directions on web mapping websites like Mapquest or Google Maps.
If one represents a nondeterministic abstract machine as a graph where vertices describe states and edges describe possible transitions, shortest path algorithms can be used to find an optimal sequence of choices to reach a certain goal state, or to establish lower bounds on the time needed to reach a given state. For example, if vertices represents the states of a puzzle like a Rubik's Cube and each directed edge corresponds to a single move or turn, shortest path algorithms can be used to find a solution that uses the minimum possible number of moves.
In a networking or telecommunications mindset, this shortest path problem is sometimes called the min-delay path problem and usually tied with a widest path problem. For example, the algorithm may seek the shortest (min-delay) widest path, or widest shortest (min-delay) path.
A more lighthearted application is the games of "Six degrees of separation|Six degrees of separation" that try to find the shortest path in graphs like movie stars appearing in the same film.
Other applications include "operations research, plant and facility layout, robotics, transportation, and Very-large-scale integration design".<ref>Danny Z. Chen. Developing Algorithms and Software for Geometric Path Planning Problems. ACM Computing Surveys 28A(4), December 1996.</ref>
CS2: Data Structures
Theory of Computation - ADT Preliminaries
Linear ADTs - Tree ADTs - Graph ADTs - Unordered Collection ADTs