AVL Trees

From

Begin

↑ Binary Trees

AVL Trees →

Named after two Russian mathematicians, G. M. Adel’son-Vel’skii and E. M. Landis who published their result in 1962, this variation of a binary search tree rebalances itself after every insertion or deletion.

An AVL Tree uses the idea that doing some work on each insertion or deletion saves a great deal of work when the tree is badly out of balance. Since the tree is always in balance or out of balance by only one level, searching an AVL tree is quite efficient ( Θ( log₂ N ), where N is the number of nodes in the tree).

AVL Behavior

Each node in an AVL tree contains information regarding the balance of the tree at that node. This information, called the balance factor, is defined as the height of the left subtree minus the height of the right subtree. Thus, when a tree is perfectly balanced, every node has a balance factor that equals zero.

Whenever a node is inserted or deleted into an AVL tree, the balance factor for each node along the path from the root to the inserted or deleted node must be recalculated. As long as the balance factor for each node is a -1, 0, or +1, no further action is taken. If a balance factor does not fall within this range, one of four type of rotations is performed that involve the out-of-balance node. The possible rotations are: (1) single right rotation, (2) single left rotation, (3) double left-right rotation, and (4) double right-left rotation. The rules for which rotation are somewhat complex, but we will look at an example of a single and a double rotation below.

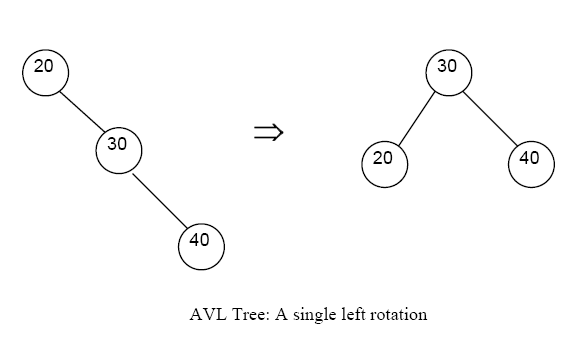
Single Left Rotation

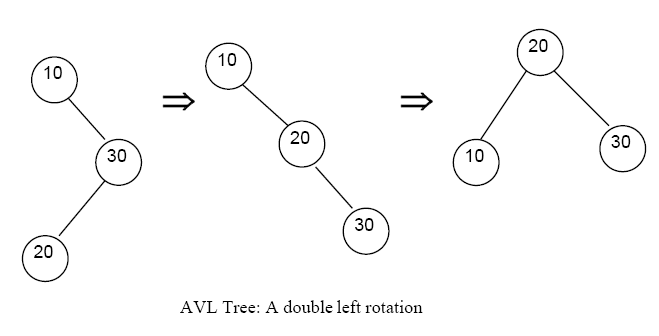
Double Left Rotation

---

---