AVL Trees
From
| ← Binary Search Trees | ↑ Binary Trees | Red-Black Trees → |
An AVL tree is a self-balancing binary search tree, and it is the first such data structure to be invented.[1] In an AVL tree, the heights of the two child subtrees of any node differ by at most one; therefore, it is also said to be height-balanced. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where n is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.
The AVL tree is named after its two inventors, G.M. Adelson-Velskii and E.M. Landis, who published it in their 1962 paper "An algorithm for the organization of information."
Contents |
AVL Behavior
Each node in an AVL tree contains information regarding the balance of the tree at that node. This information, called the balance factor, is defined as the height of the right subtree minus the height of the left subtree. Thus, when a tree is perfectly balanced, every node has a balance factor that equals zero. Recall that the height of a binary tree is the maximum path length from the root to a leaf. A single-node binary tree has height 0, and we will define an empty binary tree (or a null subtree) to have height -1.
An AVL tree is a binary search tree in which every node is height balanced, that is, the difference in the heights of its two subtrees is at most 1. An equivalent definition, then, for an AVL tree is that it is a binary search tree in which each node has a balance factor of -1, 0, or +1. Note that a balance factor of -1 means that the subtree is left-heavy, and a balance factor of +1 means that the subtree is right-heavy.
Whenever a node is inserted or deleted into an AVL tree, the balance factor for each node along the path from the root to the inserted or deleted node must be recalculated. As long as the balance factor for each node is a -1, 0, or +1, no further action is taken. If a balance factor does not fall within this range, one of four type of rotations is performed that involve the out-of-balance node. The possible rotations are: (1) single right rotation, (2) single left rotation, (3) double left-right rotation, and (4) double right-left rotation.
AVL Tree Right Rotations
These rotations are required when a node with balance factor -1 changes to -2 as a result of a new node being inserted somewhere in it's left subtree. Change is needed at this node as it is now out of balance. The tree is restored to an AVL tree by using a one of the right rotations.
A Single Right Rotation is used when the node that is out of balance to the left (balance factor <= -2), and the left subtree is left heavy (balance factor = -1). This is sometimes called the Left-Left case: 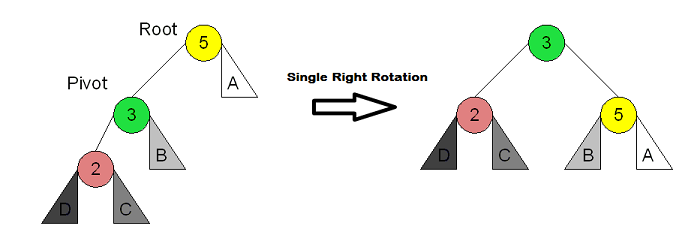
A Double Right Rotation is used when the node that is out of balance to the left (balance factor <= -2), and the left subtree is right heavy (balance factor = 1). The double-right rotation is a single-left rotation of the left subtree followed by a single right rotation of the node that is out of balance. This is sometimes called the Left-Right case: 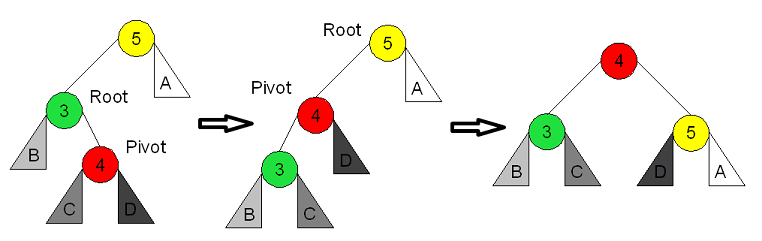
AVL Tree Left Rotations
These rotations are required when a node with balance factor 1 changes to 2 as a result of a new node being inserted somewhere in its right subtree. Change is needed at this node as it is now out of balance. The tree is restored to an AVL tree by using a one of the left rotations.
A Single Left Rotation for subtrees that are out of balance to the right (balance factor >= 2), and the right subtree is right heavy (balance factor = 1). This is sometimes called the Right-Right case: 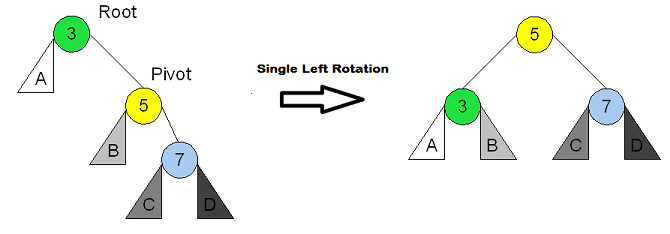
Double Left Rotation for subtrees that are out of balance to the right (balance factor >= 2) and the right subree is left heavy (balance factor = -1). The double-left rotation is a single-right rotation of the right subtree followed by a single left rotation of the node that is out of balance. This is sometimes called the Left-Right case: 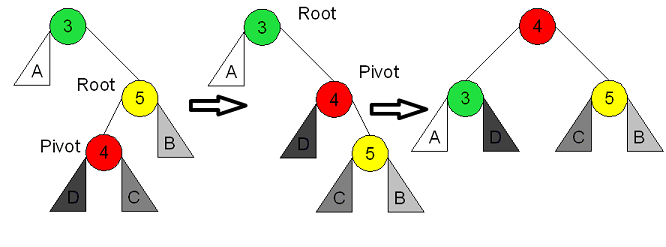
AVL Tree time analysis
Here is a summary of what Tenenbaum and Augenstein say about efficiency. See their text for more details.
The maximum height of an AVL tree is 1.44 * lg n, which is an O(lg n) function. This means that in the worst possible case, a lookup in a large AVL tree needs no more than 44% more comparisons than a lookup in a completely balanced tree. Even in the worst case, then, AVL trees are efficient; they still have O(lg n) lookup times. On average, for large n, AVL trees have lookup times of (lg n) + 0.25, which is even better than the above worst case figure, though still O(lg n). On average, a rotation (single or double) is required in 46.5% of insertions. Only one (single or double) rotation is needed to readjust an AVL tree after an insertion throws it out of balance.
CS2: Data Structures
Theory of Computation - ADT Preliminaries
Linear ADTs - Tree ADTs - Graph ADTs - Unordered Collection ADTs
