Common Graph Algorithms
From
(→Algorithm) |
(→Shortest Path algorithms) |
||
| Line 47: | Line 47: | ||
}} | }} | ||
{{graph search algorithm}} | {{graph search algorithm}} | ||
| - | '''Dijkstra's algorithm''', conceived by Dutch | + | '''Dijkstra's algorithm''', conceived by Dutch computer scientist Edsger Dijkstra in 1959, is a graph search algorithm that solves the single-source shortest path problem for a graph with nonnegative edge path costs, producing a shortest path tree. This algorithm is often used in routing. |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | For a given source vertex (node) in the graph, the algorithm finds the path with lowest cost (i.e. the shortest path) between that vertex and every other vertex. It can also be used for finding costs of shortest paths from a single vertex to a single destination vertex by stopping the algorithm once the shortest path to the destination vertex has been determined. For example, if the vertices of the graph represent cities and edge path costs represent driving distances between pairs of cities connected by a direct road, Dijkstra's algorithm can be used to find the shortest route between one city and all other cities. As a result, the shortest path first is widely used in network routing protocols, most notably IS-IS and OSPF (Open Shortest Path First). | ||
==Algorithm== | ==Algorithm== | ||
Revision as of 11:25, 2 June 2009
| ← Variations of Graph ADTs | ↑ Contents: CS2 | End |
Contents |
Graph Traversals
Graph breadth-first traversal is implemented using the same algorithm as with the tree ADT, with the addition that you have to check for nodes that have previously added to the work queue, usually by marking the node somehow. This requirement is needed as graphs may be cyclic; which would cause infinite looping in this algorithm without this check.
A Breadth-First Traversal has the following algorithm (for connected graphs):
Let Q be a queue that holds vertices (nodes) and let P be a pointer to a vertex (node).
Choose and enqueue a starting vertex from the graph.
WHILE the queue is not empty do the following
dequeue a vertex and assign it to P
visit the vertex pointed to by P
FOREACH child of the vertex that has not been previously MARKED
enqueue the child
ENDFOR
ENDWHILE
A breadth-first traversal is often called a level-order traversal. Note that we can also change the above algorithm to a depth-first traversal by simply changing from a Queue to a Stack (and the enqueues/dequeues to pushes/pops)
Minimum Spanning Tree algorithms
Given a connected graph, undirected graph, a spanning tree of that graph is a subgraph which is a tree and connects all the vertices together. A single graph can have many different spanning trees. We can also assign a weight to each edge, which is a number representing how unfavorable it is, and use this to assign a weight to a spanning tree by computing the sum of the weights of the edges in that spanning tree. A minimum spanning tree (MST) or minimum weight spanning tree is then a spanning tree with weight less than or equal to the weight of every other spanning tree. More generally, any undirected graph (not necessarily connected) has a minimum spanning forest, which is a union of minimum spanning trees for its connected components.
One example would be a cable TV company laying cable to a new neighborhood. If it is constrained to bury the cable only along certain paths, then there would be a graph representing which points are connected by those paths. Some of those paths might be more expensive, because they are longer, or require the cable to be buried deeper; these paths would be represented by edges with larger weights. A spanning tree for that graph would be a subset of those paths that has no cycles but still connects to every house. There might be several spanning trees possible. A minimum spanning tree would be one with the lowest total cost.
Shortest Path algorithms
{ class="infobox " cellspacing="5" style="width: 22em; text-align: left; font-size: 88%; line-height: 1.5em; background:#fff6d9" + class="" style="font-size: 125%; font-weight: bold; "Common Graph Algorithms - colspan="2" class="" style="text-align:center; " 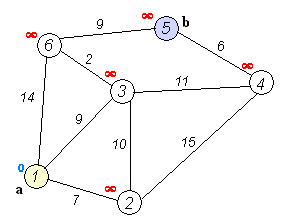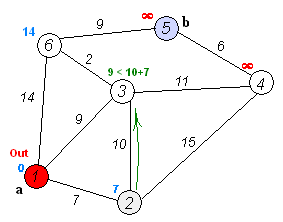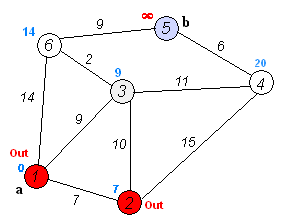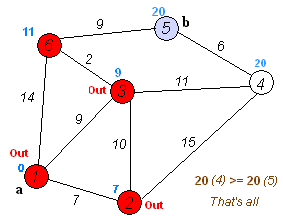
Dijkstra's algorithm runtime - ! style=""Class
class="" style=""Search algorithm
- ! style=""Data structure
class="" style=""Graph
- ! style=""Worst case performance
class="" style=""O( | E | + | V | log | V | )
- style="text-align:right;" colspan=2"Template:Tnavbar }
Template:Graph search algorithm Dijkstra's algorithm, conceived by Dutch computer scientist Edsger Dijkstra in 1959, is a graph search algorithm that solves the single-source shortest path problem for a graph with nonnegative edge path costs, producing a shortest path tree. This algorithm is often used in routing.
For a given source vertex (node) in the graph, the algorithm finds the path with lowest cost (i.e. the shortest path) between that vertex and every other vertex. It can also be used for finding costs of shortest paths from a single vertex to a single destination vertex by stopping the algorithm once the shortest path to the destination vertex has been determined. For example, if the vertices of the graph represent cities and edge path costs represent driving distances between pairs of cities connected by a direct road, Dijkstra's algorithm can be used to find the shortest route between one city and all other cities. As a result, the shortest path first is widely used in network routing protocols, most notably IS-IS and OSPF (Open Shortest Path First).
Algorithm
Let's call the node we are starting with an initial node. Let a distance of a node Y be the distance from the initial node to it. Dijkstra's algorithm will assign some initial distance values and will try to improve them step-by-step.
- Assign to every node a distance value. Set it to zero for our initial node and to infinity for all other nodes.
- Mark all nodes as unvisited. Set initial node as current.
- For current node, consider all its unvisited neighbours and calculate their distance (from the initial node). For example, if current node (A) has distance of 6, and an edge connecting it with another node (B) is 2, the distance to B through A will be 6+2=8. If this distance is less than the previously recorded distance (infinity in the beginning, zero for the initial node), overwrite the distance.
- When we are done considering all neighbours of the current node, mark it as visited. A visited node will not be checked ever again; its distance recorded now is final and minimal.
- Set the unvisited node with the smallest distance (from the initial node) as the next "current node" and continue from step 3
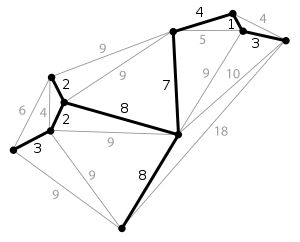
In graph theory, the shortest path problem is the problem of finding a path between two vertices (or nodes) such that the sum of the weights of its constituent edges is minimized. An example is finding the quickest way to get from one location to another on a road map; in this case, the vertices represent locations and the edges represent segments of road and are weighted by the time needed to travel that segment.
Formally, given a weighted graph (that is, a set V of vertices, a set E of edges, and a real-valued weight function f : E → 'R), and one element v of V, find a path P from v to each v of V so that
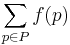
is minimal among all paths connecting v to v' .
The problem is also sometimes called the single-pair shortest path problem, to distinguish it from the following generalizations:
- The single-source shortest path problem, in which we have to find shortest paths from a source vertex v to all other vertices in the graph.
- The single-destination shortest path problem, in which we have to find shortest paths from all vertices in the graph to a single destination vertex v. This can be reduced to the single-source shortest path problem by reversing the edges in the graph.
- The all-pairs shortest path problem', in which we have to find shortest paths between every pair of vertices v, v in the graph.
These generalizations have significantly more efficient algorithms than the simplistic approach of running a single-pair shortest path algorithm on all relevant pairs of vertices.
Applications of Shortest Path Algrithms
Shortest path algorithms are applied to automatically find directions between physical locations, such as driving directions on web mapping websites like Mapquest or Google Maps.
If one represents a nondeterministic abstract machine as a graph where vertices describe states and edges describe possible transitions, shortest path algorithms can be used to find an optimal sequence of choices to reach a certain goal state, or to establish lower bounds on the time needed to reach a given state. For example, if vertices represents the states of a puzzle like a Rubik's Cube and each directed edge corresponds to a single move or turn, shortest path algorithms can be used to find a solution that uses the minimum possible number of moves.
In a networking or telecommunications mindset, this shortest path problem is sometimes called the min-delay path problem and usually tied with a widest path problem. For example, the algorithm may seek the shortest (min-delay) widest path, or widest shortest (min-delay) path.
A more lighthearted application is the games of "Six degrees of separation|Six degrees of separation" that try to find the shortest path in graphs like movie stars appearing in the same film.
Other applications include "operations research, plant and facility layout, robotics, transportation, and Very-large-scale integration design".<ref>Danny Z. Chen. Developing Algorithms and Software for Geometric Path Planning Problems. ACM Computing Surveys 28A(4), December 1996.</ref>
CS2: Data Structures
Theory of Computation - ADT Preliminaries
Linear ADTs - Tree ADTs - Graph ADTs - Unordered Collection ADTs